Статистические методы обработки данных в экологии: Методические рекомендации по изучению дисциплины, страница 11

1.  В каких случаях используются непараметрические методы факторного анализа?

2.  Какая статистика используется в ранговом однофакторном анализе для проверки однородности некоторых выборок?

3.  Как производится ранжирование данных в ранговом однофакторном анализе?

4.  Какая статистика используется в ранговом двухфакторном анализе?

5.  Как производится ранжирование данных в ранговом двухфакторном анализе?

Тема 6. Корреляционный анализ

В результате изучения данной темы студент должен иметь представление:

-  о задачах корреляционного анализа;

знать:

-  сущность коэффициента корреляции и корреляционного отношения, частных коэффициентов корреляции, ранговых коэффициентов корреляции;

и уметь использовать:

-  методы расчета корреляционных зависимостей.

6.1 Методические рекомендации по изучению данной темы

Сначала ознакомьтесь с основными теоретическими сведениями приведенными выше. Затем тщательно изучите материал, изложенный в главе 7 учебного пособия. Если после изучения учебного пособия вам остались непонятны некоторые вопросы, обратитесь к рекомендуемой литературе. Затем ответьте на вопросы для самоконтроля. Проведите корреляционный анализ для данных представленных в задании 10 контрольной роботы.

6.2 Основные теоретические сведения

Задачи корреляционного анализа

Прежде чем приступить к установлению вида функциональной зависимости между переменными величинами, исследователь должен убедиться в том, что между ними действительно существует взаимосвязь. Эта задача решается путем проведения корреляционного анализа, включающего:

1)  выбор показателя статистической связи между анализируемыми переменными;

2)  оценку значения этого показателя по имеющимся экспериментальным данным;

3)  проверку статистической гипотезы о том, что значение показателя значимо отличается от нуля.

Выбор показателя парной связи

Коэффициент корреляции r_xy характеризует вероятностную линейную зависимость между двумя величинами Х и Y:

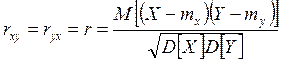
Формально этот коэффициент можно вычислить для любой системы случайных величин (Х, Y), однако только в случае системы с нормальным распределением он имеет четкий смысл характеристики тесноты связи. Во всех остальных случаях коэффициент корреляции можно использовать лишь в качестве одной из возможных характеристик степени тесноты связи.

При наличии между Х и Y нелинейной зависимости коэффициент корреляции недооценивает степень тесноты связи и даже может быть равен нулю. В таких случаях в качестве показателя тесноты связи можно использовать корреляционное отношение, квадрат которого определяется следующим образом:

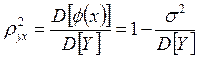
где  – составляющая общей дисперсии , обусловленная функциональной зависимостью между Х и Y; σ² – дисперсия, обусловленная влиянием на Y других факторов (в предложении, что она не зависит от значений, принимаемых Х).

Аналогично определяется квадрат корреляционного отношения ρ_xy² переменной Х и Y, при этом между ρ_yx² и ρ_xy² нет какой-либо простой зависимости.

Положительный корень из ρ_yx² носит название корреляционного отношения. В общем случае ρ_yx² и r² связаны неравенством

.

Итак, в качестве показателя статистической связи между двумя случайными переменными  Х и Y следует выбрать корреляционное отношение, если закон распределения системы (X,Y) вызывает сомнение. Если же можно с большой степенью уверенности считать закон распределения системы (X,Y) нормальным, то следует использовать коэффициент корреляции.

Оценка показателей тесноты связи

Пусть в результате эксперимента получены n выборочных значений случайной величины (X,Y): (x_i,y_i), i = 1, ..., n. Общую картину взаимной изменчивости можно получить, изобразив все точки на координатной плоскости. Это изображение называют корреляционным полем, по его виду иногда можно сделать предположение о наличии и характере связи между Х и Y. Оценка корреляции имеет вид:

,

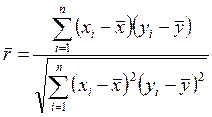где

;   .

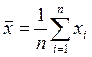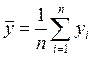Если при x_i есть повторяющиеся с частотой n_i значения Y, т.е. данные имеют вид (x_i,y_ij), j = 1, ..., n; i=1, ..., n, 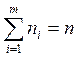, то