Статистические методы обработки данных в экологии: Методические рекомендации по изучению дисциплины, страница 13

Сначала ознакомьтесь с основными теоретическими сведениями приведенными выше. Затем тщательно изучите материал, изложенный в главе 8 учебного пособия. Если после изучения учебного пособия вам остались непонятны некоторые вопросы, обратитесь к рекомендуемой литературе. Затем ответьте на вопросы для самоконтроля. Проведите регрессионный анализ для данных представленных в задании 10 контрольной роботы.

7.2 Основные теоретические сведения

Задачи регрессионного анализа

После обнаружения статистических связей между случайными переменными методами корреляционного анализа приступают к математическому описанию интересующих зависимостей. Для этого необходимо:

1)  подобрать класс функций, в котором целесообразно искать наилучшую (в определенном смысле) аппроксимацию интересующей зависимости;

2)  найти оценки неизвестных параметров, входящих в уравнение искомой зависимости;

3)  установить адекватность полученного уравнения искомой зависимости.

Функция регрессии

Функцией регрессии (или регрессией) называется зависимость математического ожидания одной случайной величины от значения, принимаемого другой случайной величиной, образующей с первой двумерную систему случайных величин.

Так функция регрессии Y на X

,

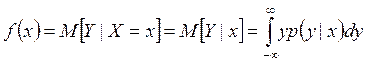а функция регрессии X на Y

.

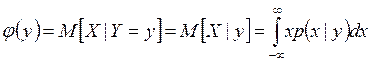Для полного определения функции регрессии необходимо знать условное распределение выходной переменной при фиксированных значениях входной переменной. Поскольку в реальной ситуации такой информацией не располагают, то обычно ограничиваются поиском подходящей аппроксимирующей функции для f(x), основываясь на статистических данных вида (x_i,y_i), i = 1,…, n. Эти данные являются результатом n независимых наблюдений y₁, …, y_n случайной величины Y при значениях входной переменной x₁, …, x_n, т. е. результатом специально организованного эксперимента. В регрессионном анализе предполагается, что значения входной переменной задаются точно.

Говоря о подходящей аппроксимации функции f(x), т.е. модели регрессии, нужно, во-первых задать класс допустимых моделей регрессии, т.е. класс функций, среди которых следует искать наилучшую аппроксимирующую функцию, и во-вторых, выбрать метод, с помощью которого будет находиться наилучшая аппроксимирующая функция из заданного класса. Одним из таких методов является метод наименьших квадратов.

Простая линейная регрессия (общий случай)

Пусть на основании результатов корреляционного анализа было установлено, что между случайными величинами X и Y имеется значимая линейная зависимость. В результате проведенного эксперимента при фиксированных значениях величины X были определены соответствующие значения случайной величины Y. Тогда модель регрессии, называемую простой (одномерной, парной) линейной моделью, можно представить в виде

,       i = 1, …, n,

где ε_i – некоррелированные между собой ошибки, имеющие нулевые математические ожидания и одинаковые дисперсии σ², a и b – постоянные коэффициенты, которые необходимо оценить по измеренным значениям отклика y_i.

Воспользуемся методом наименьших квадратов, которым оценки параметров a и b находят из условия минимизации суммы квадратов отклонений значений y_i по вертикали от “истинной” линии регрессии:

.

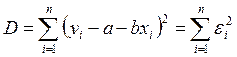Для минимизации D следует приравнять к нулю частные производные по a и b. В результате получится система двух уравнений, решение которых дает оценки параметров:

,

.

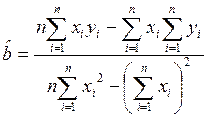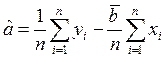Эмпирическое уравнение регрессионной прямой X на Y можно записать в виде

.

Несмещенная оценка дисперсии σ² отклонений от линии регрессии дается выражением

.

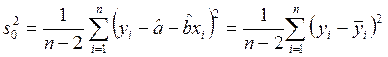Величину s₀² часто называют остаточной дисперсией.

Проверка значимости линии регрессии

Полученная оценка b≠0 может быть реализацией случайной величины, математическое ожидание которой равно нулю, т.е. может оказаться, что на самом деле никакой регрессионной зависимости нет. Для этого следует проверить гипотезу H₀: b =0 против H₁: b≠0.

Проверку значимости линии регрессии можно провести с помощью дисперсионного анализа, основанного на следующем тождестве:

.

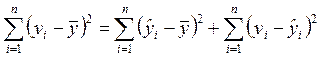Величина