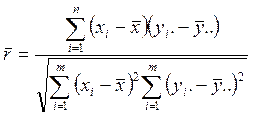Статистические методы обработки данных в экологии: Методические рекомендации по изучению дисциплины, страница 12

,

где

;         .

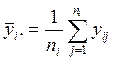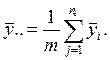Оценку квадрату корреляционного отношения можно дать только в случае, когда при x_i есть повторяющиеся значения Y. Эта оценка имеет следующий вид:

.

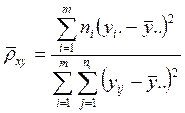Проверка значимости показателей тесноты связи

Задачи проверки некоррелированности (а значит, и независимости) нормальных случайных величин Х и Y сводится к проверке гипотезы H₀: r = 0. Статистикой критерия проверки гипотезы служит случайная величина

,

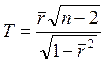которая при справедливости гипотезы H₀ распределена по закону Стьюдента с n-2 степенями свободы. При альтернативной гипотезе H₁:r ≠0 нулевая гипотеза отвергается с уровнем значимости α, если значение статистики Т больше  (α/2-процентной точки распределения Стьюдента с n-2 степенями свободы).

В предположении, что при Х=х случайная величина Y имеет нормальный закон распределения  для любого х, проверка гипотезы H₀: ρ_yx=0 (отсутствие связи Y с Х) осуществляется с использованием статистики

,

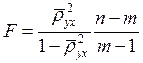имеющей распределение Фишера с m-1 и n-m степенями свободы. Если вычисленное значение статистики F окажется больше f_m-1;n-m;α, то нулевую гипотезу следует отвергнуть с уровнем значимости α, т.е. признать существование связи между X и Y.

Частные коэффициенты корреляции

При рассмотрении трех и более случайных величин коэффициенты корреляции любой пары этих случайных величин могут не дать преставления о степени связи между всеми случайными величинами. Это объясняется тем, что на закон распределения исследуемой пары могут оказывать влияние и другие рассматриваемые величины. Это обстоятельство делает необходимым введение статистического показателя связи между парой случайных величин при условии, что значения других случайных величин зафиксированы.

Обозначим выходную случайную величину Y через X₀, а остальные случайные величины через X₁, X₂,..., X_p. Предположим, что случайный вектор (X₁, X₂,..., X_p) имеет нормальный закон распределения с корреляционной матрицей

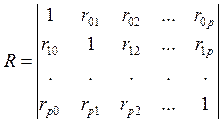
где r_ij – коэффициенты корреляции между случайными величинами X_i, X_j,
i, j= 0,1, ..., p.

Мерой линейной вероятностной зависимости между двумя случайными величинами X_i и X_j из некоторой совокупности случайных величин X₀, X₁, X₂,..., X_p, когда исключено влияние остальных, служит частный коэффициент корреляции

,

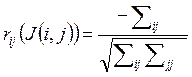где  – алгебраическое дополнение к элементу  корреляционной матрицы; J(i, j) = 0, 1, ..., p за исключением индексов i и j.

Значения точечных оценок частных коэффициентов корреляции получают подстановкой вместо коэффициентов корреляции  их выборочных значений .

Выборочный частный коэффициент корреляции распределен так же, как и выборочный парный коэффициент корреляции, поэтому для проверки его значимости используется та же статистика T, но с заменой n на n-k, где k – порядок частного коэффициента корреляции (число “мешающих” переменных).

6.3 Вопросы для самоконтроля

1.  Назовите основные задачи статистического исследования зависимостей.

2.  Что представляет собой функция регрессии случайной величины Y на случайную величину X?

3.  Дайте определение квадрата корреляционного отношения.

4.  Для каких случайных величин квадрат корреляционного отношения совпадает с квадратом коэффициента корреляции?

5.  Что такое “корреляционное поле”?

6.  Как по имеющимся данным рассчитать коэффициент корреляции между двумя случайными величинами?

7.  Как построить доверительный интервал для коэффициента корреляции?

8.  Как проверить значимость коэффициента корреляции?

9.  Какими данными следует располагать, чтобы можно было дать оценку корреляционному отношению?

10.  Что такое частный коэффициент корреляции? В чём его отличие от парного коэффициента корреляции?

Тема 7. Регрессионный анализ

В результате изучения данной темы студент должен иметь представление:

-  о задачах регрессионного анализа;

знать:

-  сущность регрессионного анализа;

и уметь использовать:

-  методы анализа регрессионных моделей.

7.1 Методические рекомендации по изучению данной темы