Статистические методы обработки данных в экологии: Методические рекомендации по изучению дисциплины, страница 5

Критерии, предназначенные для обнаружения эффектов обработки, делятся на параметрические и непараметрические. Параметрические критерии предполагают знание вида закона распределения изучаемой случайной величины и с их помощью проверяются гипотезы об изменении параметров распределения под воздействием обработки. Весьма эффективные критерии разработаны для случая нормального распределения, но они могут давать неправильные результаты при отклонении от нормальности.

Непараметрические критерии не используют предположения о виде распределения, поэтому с их помощью можно проверять только гипотезу об однородности выборок до и после обработки.

Проверка гипотез, связанных с параметрами нормально распределенных случайных величин

Проверка гипотезы о равенстве дисперсий генеральных совокупностей.

Проверка гипотезы о равенстве дисперсий двух генеральных совокупностей на основе их выборочных значений осуществляется с использованием статистики

,

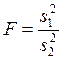которая имеет распределение Фишера (F-распределение) с числом степеней свободы n-1 и m-1, где  наибольшая из выборочных дисперсий.

Критерий проверки гипотезы H₀:  против альтернативы H₁:  сводится к следующему:

нулевая гипотеза отвергается, ес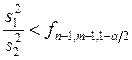ли

         или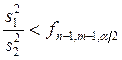    

где  и  – процентные точки F-распределения.

Сравнение средних (математических ожиданий) независимых выборок

Пусть x₁,...,x_n и y₁,...,y_m – независимые выборки из нормальных генеральных совокупностей с параметрами m_x, σ_x² и m_y, σ_y² соответственно. Рассмотрим проверку гипотезы H₀:  при альтернативной гипотезе H₁: .

Относительно параметров σ_x² и σ_y² выделим четыре варианта предположений:

а) обе дисперсии известны и равны между собой (σ_x² = σ_y² = σ²);

б) обе дисперсии известны, но не равны между собой;

в) обе дисперсии неизвестны, но предполагается, что они равны;

г) обе дисперсии неизвестны, их равенство не предполагается.

Перейдем от выборок x₁,...,x_n и y₁,...,y_m к выборочным средним  и . В соответствии со свойствами нормального распределения при справедливости гипотезы H₀ величины  и  имеют нормальные распределения с одним и тем же средним и дисперсиями σ_x²/n и σ_x²/m.

Введем статистики, основанные на выборочных средних  и  и дисперсиях σ_x² и σ_y² (если они известны) или их оценках s_x² и s_y² (если дисперсии неизвестны). Эти статистики выберем так, чтобы их распределения при гипотезе H₀ не зависели от неизвестных значений математических ожиданий. Для перечисленных выше случаев эти статистики будут иметь следующий вид:

Гипотеза H₀ отвергается на уровне значимости α, если

где  – квантиль порядка  стандартного нормального распределения.

Гипотеза H₀ отвергается на уровне значимости α, если

.

Объединенная оценка дисперсии , получается на основе объединения двух выборок в одну

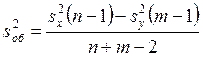
Гипотеза H₀ отвергается, если

где  – процентная точка распределения Стьюдента с n+m-2 степенями свободы.

Гипотеза H₀ отвергается, если

.

Сравнение средних двух зависимых выборок

Существует много задач, в которых две выборки взаимосвязаны в силу особенностей планирования эксперимента или потому, что избежать этой связи невозможно. Иначе говоря, существует посторонний фактор (или факторы) не относящийся к различию между выборками. Например, это имеет место, когда признаки измеряются на одном и том же объекте.

Пусть x_i1 и x_i2 – результаты измерений для i-го объекта. Чтобы учесть взаимосвязь выборок, берут соответствующие выборочные значения парами и исследуют их разности z_i = x_i1 - x_i2.

Проверяемую гипотезу можно записать в виде H₀:  или, что эквивалентно, H₀: , а альтернативную в виде H₁: .