Статистические методы обработки данных в экологии: Методические рекомендации по изучению дисциплины, страница 3

-  проверить соответствия выбранной модели закона распределения исходным данным.

2.1 Методические рекомендации по изучению данной темы

Сначала ознакомьтесь с основными теоретическими сведениями приведенными выше. Затем тщательно изучите материал, изложенный в главе 2 учебного пособия. Если после изучения учебного пособия вам остались непонятны некоторые вопросы, обратитесь к рекомендуемой литературе. Затем ответьте на вопросы для самоконтроля.

2.2 Основные теоретические сведения

Анализ резко выделяющихся наблюдений

Один из критериев для идентификации резко выделяющихся наблюдений основан на статистике

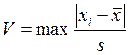
где x_i – значение наблюдения,  ­– выборочное среднее, s – среднеквадратическое отклонение:

,

.

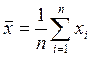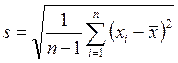Для различного числа наблюдений n и уровня значимости α составлены таблицы критических значений V_кр данной статистики. Если вычисленное значение статистики V < V_кр, то резко выделяющееся значение в выборке нельзя считать промахом и его лучше оставить.

Построение гистограммы распределения

Представление о законе распределения случайной дискретной величины дает набор относительных частот появления ее значений в выборке

С этой целью область изменения данных разбивают на m одинаковых интервалов длинной Δx и вычисляется относительная плотность попадания значений в каждый интервал:

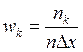,      k = 1,2,…m

где n_k – число данных, попавших в k-й интервал, n – общее число наблюдений, Δx – ширина интервала.

Диаграмму, построенную из прямоугольников с основанием Δx и высотами w_k, называют гистограммой.

Проверка соответствия выбранной модели закона распределения исходным данным

Под оценкой закона распределения понимают выбор модели закона распределения генеральной совокупности, которая не противоречит выборочным данным.

Эта задача решается с использованием критериев согласия, позволяющих с определенным уровнем значимости проверить гипотезу о том, что имеющиеся данные принадлежат генеральной совокупности с предполагаемым (теоретическим) законом распределения.

Наиболее часто приходится проверять предположение о нормальном распределении генеральной совокупности, поскольку большинство стандартных статистических методов обработки данных ориентировано на выборки из нормального распределения. С этой целью используют критерии согласия и критерии, основанные на свойствах числовых характеристик нормального распределения.

Среди критериев согласия наиболее распространенным считается критерий согласия . Применение этого критерия к выборкам из непрерывной генеральной совокупности требует предварительной группировки выборочных данных и построения гистограммы распределения ­– эмпирического аналога плотности вероятности.

В качестве меры расхождения (несоответствия) между эмпирическим и теоретическим распределением используется статистика

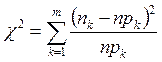
где m – число интервалов группировки выборочных данных; n_k – эмпирическая частота (число значений выборки, попавших в k-й интервал группирования); n – объем выборки; p_k – вероятность нахождения в k-м интервале случайной величины с теоретическим распределением, которая вычисляется по формуле p_k = F(c_k+1)-F(c_k). Здесь c_k левая граница k-го интервала группирования, F – функция распределения теоретического распределения.

Величина np_k является теоретической частотой (числом значений, которое ожидается в k-ом интервале группирования для данного закона распределения).

При достаточно большом объеме выборки (n> 50) при справедливости предположения о том, что выборка взята из генеральной совокупности с предполагаемым распределением, статистика  распределена по закону  с числом степеней m-1-s, где s – число параметров теоретического распределения, оцененных с использованием гистограммы распределения. Если предполагаемый закон распределения нормальный, то s = 2 и число степеней свободы равно n-3.

Процедура применения критерия  сводится к следующему:

1.  Весь диапазон выборочных значений разбивается на ряд интервалов группирования Δ₁, Δ₁, … Δ_m (не обязательно одинаковой длины).