Статистические методы обработки данных в экологии: Методические рекомендации по изучению дисциплины, страница 6

Статистикой критерия проверки нулевой гипотезы служит величина

,

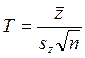которая распределена по закону Стьюдента с числом степеней свободы n-1.

Здесь  – среднее значение разностей z_i,  – выборочная дисперсия разностей.

Гипотеза H₀ отвергается на уровне значимости α, если .

Проверка гипотез об однородности двух выборок

Когда законы распределения генеральных совокупностей неизвестны, то лишено смысла говорить о сравнении параметров распределений. В этом случае можно только проверить гипотезу об однородности (идентичности) выборок, полученных до и после обработки. Для этой цели можно использовать непараметрические критерии, в частности критерии, основанные на рангах наблюдений в выборке. Эти критерии могут использоваться только в случае, когда выборки взяты из непрерывных генеральных совокупностей.

Непараметрический критерий Вилкоксона для проверки однородности двух независимых выборок

Пусть имеются две независимые выборки x₁,...,x_n и y₁,...,y_m ().

В критерии Вилкоксона для проверки гипотезы H₀:  против альтернативы H₁: , где F_x и F_y – функции распределения генеральных совокупностей X и Y, используется статистика

,

где R_j – ранги наблюдений второй выборки в общей объединенной выборке.

Проверяемая гипотеза отклоняется на уровне значимости α, если значение статистики

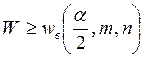     или    .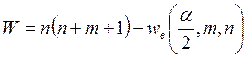

При наличии в объединенной выборке совпадающих значений всем совпавшим значениям следует приписывать одинаковый ранг, равный среднему арифметическому тех рангов, которые имели бы эти величины при несовпадении.

Непараметрический критерий Вилкоксона для проверки однородности двух зависимых выборок

Критерий Вилкоксона для парных выборочных наблюдений основан на рангах разностей наблюдений в паре.

Порядок применения критерия следующий.

1.  Вычисляются абсолютные разности наблюдений в паре:

,           i = 1,…,n

2.  Осуществляется ранжирование этих разностей в порядке возрастания и каждому значению ранга приписывается знак его разности.

3.  Вычисляется статистика T, образуемая суммой значений положительных рангов. При этом нулевые разности игнорируются, и объем выборки в последующих расчетах уменьшается.

4.  Проверяется, принадлежит ли вычисленное значение T статистики критической области, границы которой находятся по таблицам процентных точек распределения Вилкоксона для парных выборок.

Гипотеза об однородности выборок отклоняется на уровне значимости α в пользу альтернативной гипотезы о неоднородности выборок, ес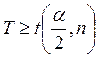ли

   или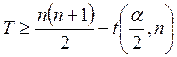   

где  – процентная точка распределения Вилкоксона для парных выборок.

3.3 Вопросы для самоконтроля

1.  Как проверить гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей по имеющимся выборкам из них?

2.  Как проверить гипотезу о равенстве математических ожиданий двух независимых нормальных генеральных совокупностей по имеющимся выборкам из них?

3.  Как проверить гипотезу о равенстве математических ожиданий двух зависимых нормальных генеральных совокупностей по имеющимся выборкам из них?

4.  Что называется рангом наблюдения в выборке?

5.  Можно ли применять ранговые критерии проверки однородности генеральных совокупностей, имеющих дискретные законы распределения?

6.  Что такое средние ранги? Когда они используются?

7.  Как проверяется гипотеза об однородности двух зависимых выборок с использованием ранговых критериев?

Тема 4. Дисперсионный анализ

В результате изучения данной темы студент должен иметь представление:

-  о задачах дисперсионного анализа;

знать:

-  основы однофакторного и двухфакторного дисперсионного анализа;

и уметь использовать:

-  методы дисперсионного анализа для решения прикладных задач.

4.1 Методические рекомендации по изучению данной темы

Сначала ознакомьтесь с основными теоретическими сведениями приведенными выше. Затем тщательно изучите материал, изложенный в главе 5 учебного пособия. Внимательно разберите решения примеров приведенных в главе 5 учебного пособия. Если после изучения учебного пособия вам остались непонятны некоторые вопросы, обратитесь к рекомендуемой литературе. Затем ответьте на вопросы для самоконтроля. Из контрольной работы выполните шестое и седьмое задания своего варианта.