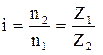Основные узлы и механизмы станков. Кинематическая структура станков, страница 8

   и   .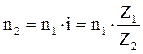

Для червячной передачи (рис. У.2,в), червяк которой имеет K заходов, а червячное колесо – Z зубьев:

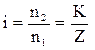   и   .

В ременных передачах (рис. У.2,г) кроме ремённозубчатых имеет место проскальзывание и это учитывают соответствующим коэффициентом (h_р[3]):

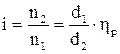   и   ,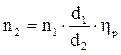

где  d₁ и d₂ – рабочие диаметры шкивов;

h_р = 1–e   и   e » 0,02 – относительное скольжение ремня.

                   а)                                       б)                                         в)                                    г)

                           

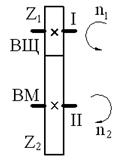
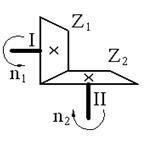
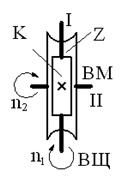
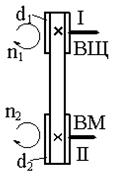
Рис. У.2. Кинематические пары для передачи вращательного движения:

а, б, в – зубчатые цилиндрическая, коническая, червячная;  г – ременная

Передачи, преобразующие вращательное движение в прямолинейное, характеризуются величиной перемещения поступательно движущегося элемента за один оборот приводного вала. Для таких передач часто увязывают скорость прямолинейного перемещения ведомого звена (v,  S) с частотой вращения (n) ведущего.

Эта зависимость будет:

- для винтовой передачи с однозаходным винтом (рис. У.3,а) – S = t×n,

    с многозаходным винтом – S = Н×n= K×t×n,

где  t и Н – шаг и ход винта;

       K – число его заходов;

- для зубчато-реечной и червячно-реечной передач (рис. У.3,б,в), соответственно,

S = t×Z×n = p×m×Z×n  и  S = t×K×n = p×m×K×n,

где  t и m – шаг и модуль зацепления;

       Z – число зубьев реечного колеса;

       K – число заходов червяка.

         а)                                                                        б)                                                       в)

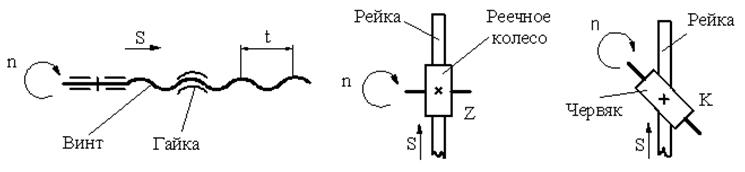
Рис. У.3. Кинематические пары для преобразования вращательного движения в поступательное:

а – винтовая;  б – зубчато-реечная; в – червячно-реечная

Вращательное движение преобразуется в прямолинейное также с помощью других передач и ряда механизмов (кривошипно-шатунных, кривошипно-кулисных, кулачковых и др.).

2.2.1.3 Совокупность передач привода определяет движение рабочих органов, т.е. кинематику их, и её называют кинематической цепью. В кинематические цепи могут входить как отдельные передачи, так и группы передач (групповые передачи).

Произвольный пример кинематической цепи, состоящей из клиноременной, четырёх зубчатых и цепной передач, приведён на рис. У.4.

Рис. У.4. Пример кинематической цепи

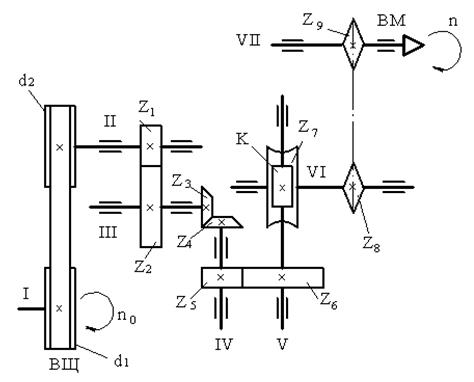
Полное передаточное отношение  кинематической цепи равно произведению передаточных отношений всех кинематических пар, составляющих цепь.

Полное передаточное отношение I кинематической цепи, показанной в качестве примера на рис. У.4, будет равно:

,

здесь Z₈ и Z₉ – числа зубьев звёздочек цепной передачи.

Направление передачи движения записывается в виде т.н. расчётного перемещения или расчётных перемещений конечных звеньев.

Так, если n_о и n – частоты вращения ведущего и ведомого валов или начального и конечного звеньев кинематической цепи, то расчётное перемещение представляют в виде: n_о®n. А если n_о и S – частота вращения ведущего вала кинематической цепи и скорость перемещения ведомого звена – гайки винтовой передачи шага t, то расчётное перемещение будет: n_о®S(подробнее см. п. 3.2).

Очевидно, в первом случае – n = n_о×I, а во втором – S = n_о×I×t.

То или иное из этих или им подобных выражений с подробно расписанной правой частью (т.е. вместо I – произведение передаточных отношений всех кинематических пар, составляющих цепь, в виде обозначений шестерён, шкивов или конкретных чисел зубьев шестерён, диаметров шкивов, в последнем случае – и конкретных значений частот вращения, шагов резьб и т.д.) называют уравнением кинематического баланса.

Для приведённой выше кинематической цепи уравнение кинематического баланса в общем виде и в предположительно возможном числовом будет:

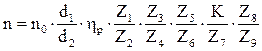  и 

Уравнение кинематического баланса позволяет определить перемещение конечного звена в зависимости от перемещения начального звена и полного передаточного отношения кинематической цепи, связывающей эти звенья, а при наличии передач, преобразующие вращательное движение в прямолинейное – и их параметров.