Основные узлы и механизмы станков. Кинематическая структура станков, страница 29

Числа зубьев некоррегированных колёс, исходя из условия отсутствия подрезания при их изготовлении и из конструктивных соображений, не следует принимать менее

Z_min=(17-)20-22.

Числа зубьев в группе передач, содержащей шестерни одинакового модуля, можно определить различными способами, и в том числе:

- способом наименьшего общего кратного;

- упрощенным способом;

- с помощью логарифмической линейки;

- по специальным таблицам.

Рассмотрим суть упрощенного способа расчёта чисел зубьев.

Пусть  в  группе  передач    при  этом    и

    Т.к.    а  

то     или       Приняв 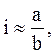   получим:

  и                                               (3.1)

При расчёте чисел зубьев принимают Z₁=Z_min, определяют 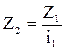  и SZ=Z₁+Z₂; обычно SZ£120. Затем определяют все остальные числа зубьев по формулам (3.1).

Пример. Определить числа зубьев передач группы на три скорости, представленной на фрагменте ДЧВ (рис. У.13,а), φ=1,26.

.

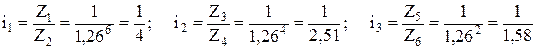Принимаем Z₁=20, тогда Z₂=20:(1/4)=80 и SZ=20+80=100;

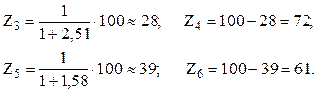
Подсчитанные числа зубьев проставляем на ДЧВ рис. У.13.б).

3.9.4 Особенности расчёта приводов со сменными обратимыми зубчатыми колёсами

При использовании в приводе сменных колёс (см. п/п. 2.2.4.1 и рис. У.5) можно уменьшить их количество, сделав обратимыми, т.е. обеспечив с помощью, например, двух колёс   Z₁¹Z₂  (а¹б)  два передаточных отношения

 с помощью 4 колёс – 4 и т.д.

На ДЧВ группа из сменных обратимых колёс имеет симметричные лучи. Фрагмент ДЧВ для группы на четыре варианта из обратимых сменных шестерён показан на рис. У.14а. Передаточные отношения группы будут следующими:

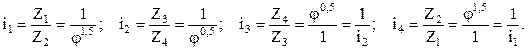
В данном случае 2 пары сменных обратимых колёс являются основной группой.

Суммы зубьев сменных колёс для станков принимают обычно равными 72,  90  или  120.

3.9.5 Особенности расчёта приводов с многоскоростными электродвигателями

Применение в приводе многоскоростного электродвигателя позволяет несколько упростить механическую часть привода и обеспечить возможность переключения скоростей на ходу.

При расчёте коробок скоростей такой двигатель играет роль первой в кинематическом плане группы передач, т.е. рассматривается как некая фиктивная "электрогруппа" со знаменателем j_э=j^р, где р – произведение чисел передач групп, предшествующих "электрогруппе" по порядку переключения для обеспечения последовательно возрастающего геометрического ряда частот вращения шпинделя.

Правильный геометрический ряд частот вращения шпинделя может быть получен при применении электродвигателей с j_э=2. К таким относятся асинхронные электродвигатели, у которых синхронные частоты вращения равны  750/1500;  1500/3000;  750/1500/3000.

С учётом отмеченного ,  откуда   .

Решение последнего выражения для ряда значений φ дано ниже:

Очевидно, "электрогруппа" при φ <2 должна быть множительной группой. К примеру, при φ=1,26 и 1,41 она должна быть I множительной с числом передач в основной 3 и 2 соответственно.

Пример. Построить структурную сетку для привода  с двухскоростным электродвигателем и φ =1,41.

При φ =1,41 "электрогруппе" должна предшествовать по порядку переключения основная группа на две скорости. Примем структурный вариант 8=2(2)·2(1)·2(4) и построим для этого случая структурную сетку (рис. У.14б), предварительно проверив, какое φ_max допускается выбранной структурой и возможна ли её реализация при заданном φ.