Очевидно:
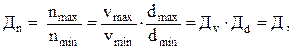
где Д (Дn) - диапазон регулирования частот вращения шпинделя.
Предельные значения частот вращения шпинделя могут быть установлены на основании результатов статистического обследования станков, аналогичных проектируемому, в реальных производственных условиях.
3.6 Регулирование частот вращения шпинделя
|
Рис. У.7.
Графическая интерпретация зависимости |
Регулирование частот вращения в диапазоне Д может быть плавным и ступенчатым. При ступенчатом регулировании в пределах от nmin до nmax возможно получение z вариантов частот вращения:
Поскольку
зависимость v от d при некотором n прямо пропорциональна ( Если, к примеру, на станке, коробка скоростей которого обеспечивает получение на шпинделе некоторого ряда частот вращения и, в том числе, частот nj и nj+1 (см. рис. У.7), требуется обрабатывать со скоростью v' деталь диаметра dk, то необходимо установить частоту nj, если – dm, то nj+1. |
При необходимости обработки детали диаметра d' скорость v' обеспечить нельзя, а можно лишь vj, либо vj+1. Последнее не рекомендуется, т.к. это связано с уменьшением стойкости инструмента.
Величина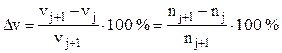 
, называемая относительным
перепадом скоростей, будет характеризовать предел возможной потери
скорости за счёт ступенчатого регулирования.
К примеру, ∆v=20 % означает, что при обработке различных деталей в зависимости от их размеров скорость резания может устанавливаться с различной степенью точности по отношению к рекомендуемой, но это отклонение не будет превосходить 20 %.
В станкостроении для распределения в заданных пределах промежуточных значений частот вращения и двойных ходов в единицу времени при ступенчатом регулировании применяют геометрические ряды, для распределения подач – геометрические и, в некоторых случаях, арифметические ряды.
3.7 Геометрический ряд частот вращения
Ряд частот вращения, содержащий z значений частот, может быть построен следующим образом:
… ; 
…;
.
Очевидно, 
где
.
Прологарифмируем последнее выражение:
откуда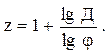 
В выражениях 
– знаменатель геометрической прогрессии,
называемый знаменателем ряда.
Очевидно: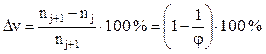 
и
для конкретного значения φ ∆v=сonst, т.е. в геометрическом
ряде обеспечивается постоянный перепад скоростей. Лучевая диаграмма для него
показана на рис. У.8.
|
Запишем в качестве примера ряд,
в котором n1=10, z=8, 10 – 20 – 40 – 80 – – 160 – 320 – 640 – 1280; в этом ряду: 10/160= 20/320= 40/640= 80/1280 =1/16. Как видно, геометрический ряд позволяет получать кратные частоты вращения. Это даёт возможность строить сложные коробки скоростей из нескольких элементарных двухваловых групповых передач, размещаемых последовательно. Впервые целесообразность применения геометрического ряда для приводов станков была обоснована русским академиком А.В. Гадолиным в 1876 году. |
Рис. У.8. Лучевая диаграмма для геометрического ряда частот вращения |
Геометрические ряды применяются также в общей стандартизации машиностроения.
3.8 Предпочтительные числа и ряды предпочтительных чисел.
Стандартные значения знаменателей геометрических рядов
Значения чисел и знаменателей геометрических рядов устанавливаются ГОСТ 8032-84.
Точные значения
знаменателей геометрических рядов определяются по формуле 
, где R = 5; 10; 20; 40; 80; 160 – число членов прогрессии
в одном десятичном интервале (например, в интервале от 1 до 10, исключая
последнее число). Буква R с этими же числами используется для обозначений
рядов: R5 – геометрический ряд с пятью членами в десятичном интервале, R10 – с
десятью и т.д.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
), какая-либо частота вращения в
прямоугольных координатах v-d представляется лучом – прямой линией, выходящей
из центра координат. График в этих координатах с совокупностью лучей,
представляющих частоты вращения (рис. У.7), иногда называют лучевой диаграммой.