В структуре z = 16 = 4(1)·2(4)·2(8)
с Д = 31,5 (т.к. ![]() то при
φ = 1,26 обеспечивается
то при
φ = 1,26 обеспечивается ![]() ) вместо xk= 8 примем xk.пер= 4 и рассмотрим построенную
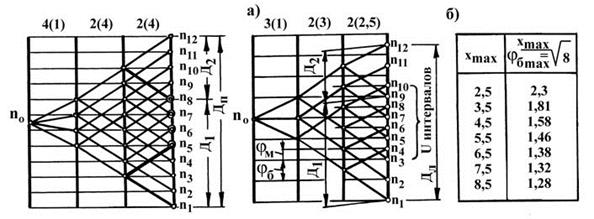
для этого случая структурную сетку (рис. 3.4).
) вместо xk= 8 примем xk.пер= 4 и рассмотрим построенную
для этого случая структурную сетку (рис. 3.4).
Как видно, каждая из ступеней n5–n8 получается двумя комбинациями передач, в результате различных частот вращения фактически обеспечивается zф = z – zпер = 16 – 4 = 12, где zпер – количество перекрытых частот вращения.
Развернутую структурную формулу можно представить в виде:
zф=12=4(1)·2(4)·2(4).
Диапазон регулирования привода с перекрытием:
![]() или (см. рис. 3.4)
или (см. рис. 3.4) ![]()
Приравняв показатели степеней в первом и втором выражениях, получим
zф = 0,5z + xk.пер, откуда xk.пер = zф – 0,5z и z = 2(zф – xk.пер).
Для структур с перекрытием φmax следует определять в последней (k-той) и предпоследней (k–1) множительных группах и принимать φ не превосходящим меньшего из двух полученных значений φmax.
В рассматриваемом случае xmax (k) = xmax (k-1) = 4, ![]() и при
φ =1,58 обеспечивается диапазон
регулирования частот вращения шпинделя
и при
φ =1,58 обеспечивается диапазон
регулирования частот вращения шпинделя ![]()
Нормальная множительная структура
на 12 вариантов z=12=3(1)·2(3)·2(6) (см. рис. 2.10) допускает ![]() и при φ =1,41 обеспечивает
и при φ =1,41 обеспечивает ![]()
Как видно, структура с перекрытием обеспечивает диапазон регулирования в 3,5 раза больший при тех же 12 фактических вариантах. Для этого потребовалось усложнить конструкцию по рис. 2.10 всего на одну передачу.
Для обеспечения в
структуре с перекрытием максимального диапазона при заданных z и кинематической
схеме следует принять φ =φmax при хk.пер = xmax (k-1). При этом, если φmax не равно какому-либо
стандартному значению, то, приняв стандартное φ<φmax, следует проверить возможность
увеличения хk.пер по формуле ![]() полученной из выражения
полученной из выражения ![]() (см.
п/п. 3.9.1.7) для данного случая.
(см.
п/п. 3.9.1.7) для данного случая.
Покажем в качестве примера, как спроектировать структуры с максимальными диапазонами на базе приводов 12=3·2·2 и 24=4·3·2:
а) zф=3(1)·2(xk-1)·2(xk.пер.), zф=3(1)·2(3)·2(xk.пер.), т.к. pk-1 =2, xmax (k-1)=xk-1=3, то принимаем xk.пер =xmax (k-1) =3.
Тогда ![]() zф=12/2+3=9 и
9=3(1)·2(3)·2(3). При φ =2
zф=12/2+3=9 и
9=3(1)·2(3)·2(3). При φ =2 ![]()
б) zф=4(1)·3(xk-1)·2(xk.пер), zф=4(1)·3(4)·2(xk.пер.),
т.к.
pk-1 ![]() 2, то xmax (k-1) = (pk-1–1) ·xk-1=(3–1)·4=8 и xk.пер=xmax(k-1)=8.
2, то xmax (k-1) = (pk-1–1) ·xk-1=(3–1)·4=8 и xk.пер=xmax(k-1)=8.
Тогда ![]() zф=24/2+8=20. При φ =1,26
zф=24/2+8=20. При φ =1,26 ![]() Если принять xk.пер=lg8/lg1,26
Если принять xk.пер=lg8/lg1,26![]() 9, то zф=24/2+9=21=4(1)·3(4)·2(9) и
9, то zф=24/2+9=21=4(1)·3(4)·2(9) и ![]()
Из всех возможных структур с перекрытием максимальный диапазон обеспечивают:
|
при φ =1,26: |
z =36; |
zф =27; |
Дп.max≈400; |
|
при φ =1,41: |
z =24; |
zф =18; |
Дп.max≈360; |
т.е. диапазон может быть увеличен примерно в 8 раз по сравнению с тем, какой обеспечивается нормальной множительной структурой.
Использование структур с перекрытием позволяет строить приводы практически на любые числа вариантов (10, 11,13, 14, 15, 17 и т.п.).
|
Рис. 3.4. Структурная сетка привода с перекрытием части ступеней скорости на 12 вариантов |
Рис. 3.5. Структурная сетка привода на 12 вариантов с составным (ломаным) геометрическим рядом (а) и таблица для определения φб.max (б) |
3.9.6.3 Применение составных (ломаных) геометрических рядов
В станках средняя часть диапазона скоростей шпинделя используется чаще, чем его крайние значения. В связи с этим можно проектировать структуры с составным (ломаным) геометрическим рядом, т.е. рядом, имеющим в различных интервалах неодинаковые знаменатели.
Удобно использовать ломаные ряды
со знаменателем φб для крайних и ![]() для
средних ступеней диапазона частот вращения шпинделя.
для
средних ступеней диапазона частот вращения шпинделя.
В качестве φб и φм могут быть приняты следующие знаменатели основных рядов 1,58 и 1,26; 1,26 и 1,12; 1,12 и 1,06; а также выборочных 2,5 и 1,58; 2 и 1,41; 1,41 и 1,18; 1,18 и 1,09.
Один из способов проектирования привода с составным (ломаным) геометрическим рядом следующий: уменьшают характеристику последней множительной группы по сравнению с расчётной величиной на 0,5·u, где u = 1, 3, 5, 7, ... – какое-либо нечетное число.
То есть xk.лом=xk–0,5·u. При pk=2 xk=z/2 и xk.лом=(z–u)/2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.