Задания на практические работы по дисциплине «Моделирование систем», страница 9

-  Использование более сложных моделей нерационально, так как точность моделей определяется, в том числе и точностью входных данных.

Поток обслуживания тоже простейший, так как выполняется одно из главных свойств простейшего потока о равенстве математического ожидания времени между заявками и среднего квадратического отклонения.

Следовательно, в задаче рассматривается простейшая СМО, то есть СМО вида (М/М/1). В данной записи не указывается емкость накопителя, так как по умолчанию предполагается, что она бесконечна. Значит, можно было бы записать вид СМО (М/М/1/∞). Данная СМО предполагает, что емкость накопителя равна бесконечности. Поэтому число состояний марковской цепи бесконечно.

Построим схему «гибели-размножения». Данная схема является бесконечной, так как число состояний марковского процесса бесконечно. Граф марковской цепи приведен на рис.26.

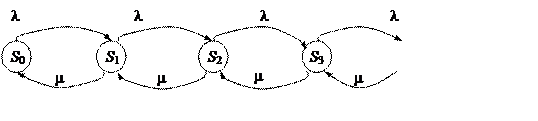Рисунок 26

Для стационарного режима функционирования данной цепи должно выполняться соотношение  Проверим его, ;  Следовательно, необходимые условия существования стационарного режима выполняются. Можно пользоваться формулами, которые будут приведены ниже. Вероятность того, что СМО будет свободна от обслуживания заявок

Вероятность того, что СМО будет занята обслуживанием k заявок  – вероятность нахождения системы в состоянии к. Например, вероятность того, что в СМО будет находиться не более одной заявки, то есть СМО будет функционировать в условиях отсутствия очереди

К другим характеристикам следует отнести:

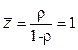  – математическое ожидание числа заявок  в системе;

 – математическое ожидание числа заявок в очереди на обслуживание;

 – математическое ожидание времени нахождения заявки в системе массового обслуживания;

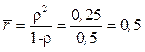 – математическое ожидание времени нахождения заявки в очереди;

Р_отк = 0. Вероятность отказа равна нулю, так как рассматривается СМО с ожиданием. Заявка никогда не получит отказ, так как емкость накопителя бесконечна.

Задача 3.3. Как изменится время на обработку цели для условий предыдущей задачи, если рассматривать не СМО с ожиданием, а СМО с отказами?

Решение: В этом случае по классификации Кендалла будет использоваться СМО вида (M/M/1/0). Ноль на четвертом знакоместе данной записи означает, что в СМО нет накопителя.

Схема «гибели-размножения» для данной СМО приведена на рис.27.

Используя соотношения, существующие для марковской цепи подобного вида, получим: ;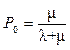

Рисунок 27

.

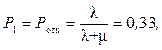
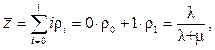
По сравнению с предыдущей задачей  стало меньше более чем в три раза. На первый взгляд это странно, так как в этом примере рассматривается худшая СМО по сравнению с предыдущей системой. В ней нет накопителя, и заявки могут получить отказ с достаточно большой вероятностью. В чем причина таких результатов?

Такие результаты становятся понятны, если учесть, что в предыдущем примере учитывается время на обслуживание всех заявок,  а в этом примере – только тех заявок, которые получат обслуживание. Следовательно, в первом случае  учитывает и время нахождения заявки в очереди, и время нахождения заявки в канале. Во втором случае учитывается только время нахождения заявки в канале. 

Следует учесть, что обе задачи не полностью соответствуют реальным условиям функционирования оператора. Оператор, обслуживая заявки, может одновременно обслуживать несколько заявок в условиях небольшой очереди на обслуживание. Однако число обслуживаемых целей и емкость накопителя определяются индивидуальными особенностями оператора.

Задача 3.4. Информационная система принимает информацию от четырех различных систем.

Параметры входного потока и потока обслуживания при решении задач сбора и обработки информации сведены в табл. 7.

Таблица 7