Задания на практические работы по дисциплине «Моделирование систем», страница 10

Определить характеристики СМО при допущении, что используется модель простейшей СМО.

Решение: Следует заметить, что входные потоки простейшие и, следовательно, их сумма, суммарный входной поток также является простейшим. Поток обслуживания, в общем случае не является простейшим, так как он получается взвешенным суммированием четырех простейших потоков обслуживания. Однако если предположить, что веса для каждого потока обслуживания одинаковы, то получается простейший поток обслуживания с параметром

Построим Q-схему для решения данной задачи (рис.28).

Рисунок 28

Так как в условии задачи предполагалось, что будет использована простейшая СМО, то в данной схеме приведен один канал обслуживания и накопитель бесконечной емкости.

Схема «гибели-размножения» приведена на рис.29.

 

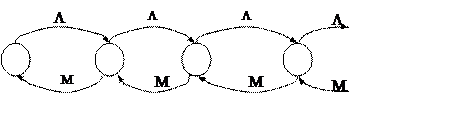Рисунок 29

Здесь указан параметр суммарного входного потока L.

,

,

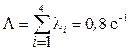r=L/M=0,72 с^-1<1,

,

Задача 3.5. Как изменится математическое ожидание времени обработки заявки в СМО, если интенсивность входного потока по сравнению с условиями предыдущей задачи увеличится. Новое значение интенсивности входного потока L=1,0 с^-1 .

Решение:

r=L/M=0,91,

,

.

Следовательно, математическое ожидание времени обработки заявки СМО увеличилось втрое. Если, например,  добавить еще одну РЛС с l=0,2с^-1, т.е. интенсивность потока увеличена немного, вместе с тем время обслуживания сразу увеличивается в несколько раз. Этот пример показывает, что очень важно правильно подбирать средства обработки, чтобы СМО работала эффективно.

Представим графики зависимости  от L при фиксированном значении M=1,1 с^-1 (рис.30).

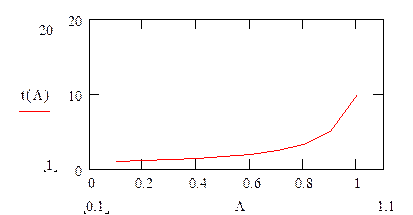
Рисунок 30

Из графика видно, что при малых L обслуживание эффективно – т.е. значение математического ожидания времени обработки заявки мало. При увеличении L наступает резкое повышение данного значения, СМО переходит на неэффективный режим функционирования. В этом случае надо увеличивать М (т.е. увеличивать вычислительные мощности средств обработки). Но здесь   тоже есть “подводные камни”, так как если увеличивать вычислительные мощности в n раз, то по закону Гроша быстродействие увеличится в . Например, если выбрать новую ЭВМ с в 100 раз большей вычислительной мощью, то быстродействие увеличится всего в 10 раз.

Задача 3.6.  Два входящих потока с одинаковыми интенсивностями l₁=l₂=0,45 мин^-1 обслуживают два одинаковых канала m₁=m₂=0,5 мин^-1. Оценить, что выгоднее – каждому каналу обслуживать свой поток  или обоим каналам обслуживать суммарный поток  L=l₁+l_2.

В качестве интерпретации такой задачи можно рассмотреть две кассы железнодорожных билетов, в которые организуются две отдельные очереди или одна суммарная очередь желающих приобрести железнодорожные билеты.

Графическое представление данной задачи для обоих вариантов представлено ниже на рис.31.

                    Вариант А                                                        Вариант В

Рисунок 31

Решение: Рассмотрим отдельно два варианта.

Вариант А предполагает раздельное обслуживание своей очереди одним каналом.  Q-схема для каждого из каналов для данного варианта будет иметь вид, как показано на рис.32.

	l1

 

    

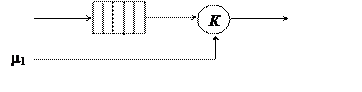
Рисунок 32

Здесь приведена простейшая система массового обслуживания. Схема «гибели-размножения» в этом случае является бесконечной и для одного канала приведена на рис.33.

 

Рисунок 33

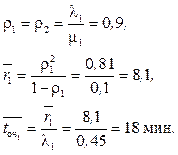
Вариант В, в котором предполагается обслуживание суммарной очереди двумя каналами. Для данного варианта Q-схема будет иметь вид, как показано на рис.34.

 

Рисунок 34

В данном случае имеем дело с двухканальной СМО с бесконечной очередью, то есть СМО вида СМО (M/M/2). Схема «гибели-размножения» для данной СМО приведена на рис.35.

 

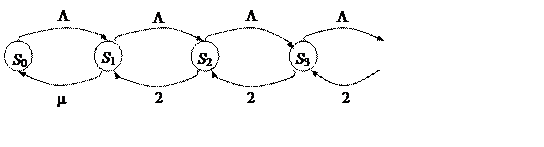Рисунок 35

На данном рисунке приняты обозначения: m=m₁=m₂,  L=l₁+l₂.