Задания на практические работы по дисциплине «Моделирование систем», страница 12

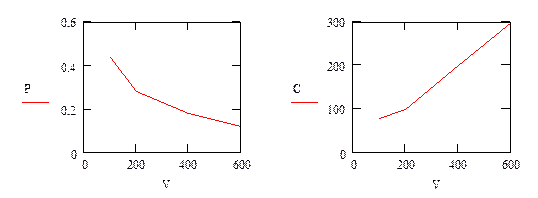
Рисунок 40

Построим новый график зависимости вероятности отказа от цены принтера. Данный график приведен на рис.41.

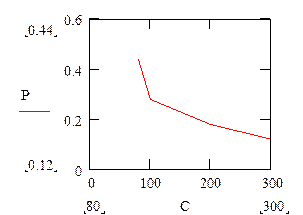
Рисунок 41

Так как при выборе принтера нужно обеспечить и малое значение вероятности отказа и  низкую цену принтера, то нет ни одного принтера, наилучшего по обоим показателям. По существу данный график определяет  множество недоминируемых альтернатив – множество Парето. Возникает проблема многокритериальности. Для ее решения необходимо перейти от вектора показателей к одному показателю, то есть необходимо произвести свертку частных показателей в один общий скалярный показатель.

Сворачивать можно по-разному. Одним из самых простых способов свертки является использование аддитивной формулы для получения одного показателя:

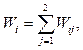
где W_i1  –  ценаi-го принтера;

W_i2 – вероятность отказа в исполнении документа i- м принтером.

Так как и цену, и вероятность отказа нужно уменьшать, то лучше будет тот принтер, у которого значение данного показателя будет меньше.

Но здесь  не все просто. Так, например, если для одного принтера W₁₁=98,  W₁₂ = 1, то по формуле свертки получим W₁= 99. Если для другого принтера W₂₁ = 100, W₂₂ = 0, то  W₂= 100. Таким образом, получаем, что первый принтер, который не способен исполнить ни одного документа, будет выбран по данному показателю. Это происходит из-за того, что показатели W_i1  и W_i2  – показатели разного порядка. Поэтому для их использования необходимо выполнить операцию нормирования, приведя значения показателей к одному диапазону возможных значений, а именно к интервалу

При решении данной задачи следует иметь в виду, что второй показатель является вероятностным. Значит, он уже нормирован. Для первого показателя предложим  два способа. В первом способе за максимум равный единице следует взять максимальную цену из всех  рассматриваемых альтернатив:

 ,

где W_iн1 – нормализованное значение показателя.

Второй способ предусматривает, что за максимум равный единице следует взять цену самого дорогого из вообще существующих принтеров:

.

В том случае, если в качестве эталона используется самый дешевый из существующих принтеров, то приведенные формулы изменятся:

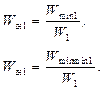
Для решения задачи будем использовать первый способ. В этом случае после нормировки получим нормализованные цены:

W_1H1 = 0,27,

W_2H1 = 0,33,

W_3H1 = 0,67,

W_4H1 = 1.

Отсюда, после использования операции свертки получим:

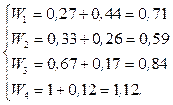
По правилу оптимизации: Таким образом, выбираем второй принтер.  W₂ = 0,59.

В данной задаче предполагалось, что и показатель надежности выполнения работы и показатель стоимости равнозначны при выборе принтера. Если это не так, то формула свертки изменится, так как под знаком сигмы добавляются весовые коэффициенты a_j.  Общий критерий в этом случае примет вид:

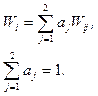
Задача 3.8. Слушатель знает три основных понятия дисциплины. Интенсивность потока забывания каждого понятия l=0,2 день^-1. При условии, что существует обучающая программа, позволяющая восстановить забытый материал, к которой курсант может подойти в любой момент и за одно одночасовое занятие восстановить одно забытое понятие, можно определить интенсивность потока восстановления забытого материала. Следовательно: m=1 час^-1. Необходимо определить вероятности того, что курсант забудет 0, 1, 2, 3 понятия.

Решение: Рассматриваемая в задаче СМО является замкнутой, так как число заявок – понятий учебной дисциплины постоянно, N=3.

Построим обобщенную Q-схему для этой задачи, которая приведена на рис.42.

 

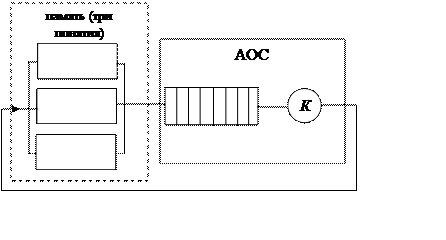Рисунок 42

В данной схеме имеется один канал К, представляющий собой автоматизированную обучающую систему, в состав которой входят три обучающие программы для  каждого из трех понятий. Память курсанта также представлена тремя каналами, в которых расположены понятия учебной дисциплины, если курсант их помнит.

В такой структуре циркулирует случайный поток, состояния которого можно задать случайным вектором:

L(t) = (L₁(t), L₂(t)),