Задания на практические работы по дисциплине «Моделирование систем», страница 4

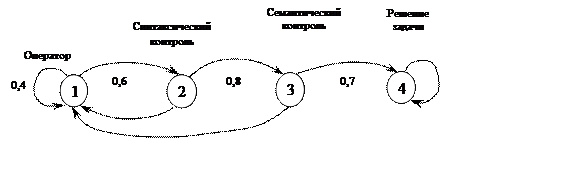
Рисунок 9

Решение: Построим матрицу вероятностей переходов для данной марковской цепи.

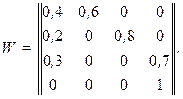
Так как продолжительность одного шага равна 5 с, то при решении задачи необходимо определить состояние марковской цепи на четвертом шаге ее функционирования. P(4) = P(0)W ⁴.

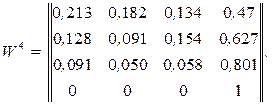
Если считать, что  то                                                                

Таким образом, решение задачи через 20 с будет завершено с вероятностью 0,47.

Задача 2.4. Граф состояний системы, в состав которой входят три автоматизированных рабочих места, приведен на рис.10.  

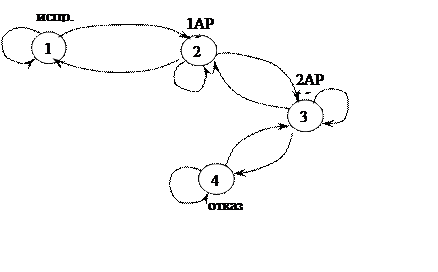
Рисунок 10

Предполагается, что во время своего функционирования автоматизированные рабочие места могут отказывать. Причем поток отказов во всех АРМ одинаков. Система отказывает, если отказали все автоматизированные рабочие места. Поэтому приведенные четыре состояния графа имеют следующую интерпретацию:

-  Первое состояние предусматривает, что все АРМ исправны.

-  Второе состояние определяет такую ситуацию, когда одно (любое) рабочее место отказывает.

-  Третье состояние описывает ситуацию отказа двух из трех автоматизированных рабочих мест.

-  Четвертое состояние относится к состоянию отказа системы.

Известна матрица переходов марковской цепи за один шаг своего функционирования.

W =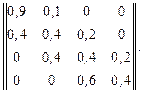

Граф и матрица марковской цепи показывают, что марковская цепь является эргодической и в ней может наступить стационарный процесс. Предположим, что система работает в стационарном режиме. Необходимо найти конечные вероятности нахождения марковской цепи в различных состояниях.

Решение: Для эргодических марковских цепей справедлива теорема о предельных вероятностях, сформулированная А. Марковым. В ней говорится о том, что с увеличением числа шагов m вероятность перехода из состояния s_i  в состояние  s_j  p(m)_ij стремится к некоторому пределу, называемому предельной или финальной вероятностью,   Ее физический смысл заключается в том, что вероятность попадания случайного процесса в состояние s_i не зависит от его начального состояния. Таким образом, такие цепи «забывают прошлое», не имеют предыстории. Процесс становится стационарным и его поведение определяется только матрицей переходов.

На основании уравнения Колмогорова  Однако, в соответствии с теоремой о предельных вероятностях, для больших m P(m+1)=P(m). Тогда уравнение Колмогорова может быть записано в виде  Данное уравнение представлено в матричной форме. Оно задает не одно, а систему n  однородных алгебраических уравнений с неизвестным вектором P, определяющим вероятности нахождения процесса в различных состояниях. Так как система является однородной и , то она имеет тривиальное решение: P=0. Такое решение является недопустимым, так как  эргодический процесс должен быть в каком-либо состоянии, т. е. вероятности должны иметь ненулевое значение. События его нахождения в различных состояниях образуют полную группу событий. Поэтому  Данное уравнение называется уравнением нормировки. Оно должно быть учтено при решении системы уравнений. Так как в системе уже имеется  n уравнений, то для ее решения необходимо одно из уравнений заменить уравнением нормировки. Тогда эта система перестанет быть однородной и ее решение не будет тривиальным.

После необходимых преобразований получим

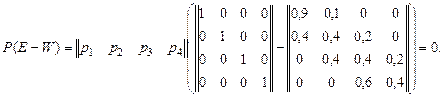
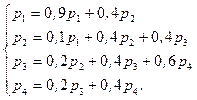
После чего будет получено нетривиальное решение.

Задача 2.5 Электрическое устройство состоит из двух узлов, которые могут заменять друг друга. Для работы необходимо, чтобы работал хотя бы один из двух узлов. Интенсивность потока отказов в каждом узле l. Интенсивность потока восстановления m. Предполагается неограниченное восстановление, при котором могут одновременно восстанавливаться все отказавшие узлы.

Данная задача предусматривает использование марковских цепей с непрерывным временем. Необходимо построить граф такой марковской цепи, в предположении, что все потоки являются простейшими.