Задания на практические работы по дисциплине «Моделирование систем», страница 2

Решение: Будем считать, что результатом сканирования является входной сигнал о наличии или отсутствии данного слова. Поэтому множество Единичное значение выходного сигнала свидетельствует о завершении сканирования слова. Процесс сканирования завершается, если обнаружен символ пробела. Поэтому входное множество имеет вид: Здесь пробел обозначен словом space, а любой другой символ словом other. Так как распознаваемое слово состоит всего из трех букв, а также конец любого слова отмечается пробелом, то автомат решает свою задачу максимально за три шага работы и  имеет три состояния;  Рассмотрим автомат Мили и будем использовать графический способ задания автомата. Данный граф будет иметь вид, как показано на рис.3.

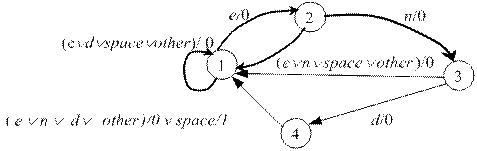
Рисунок 3

Задача 1.4.  Необходимо автомат Мура представить автоматом Мили.

Пусть автомат Мура задан графом, который приведен на рис.4.

Рисунок 4

Решение: Воспользуемся также другими способами задания автомата. В случае табличного способа используются две таблицы:переходов (табл.1 и выходов, табл.2) или одна совмещенная таблица. В них строками являются состояния автомата s_k, а столбцами входные сигналы x_i. На пересечении k-й строки i-го столбца помещается соответствующее значение  для таблицы переходов или для таблицы выходов. Так как для автомата Мура значения выходного сигнала не зависят от значения входного сигнала, поэтому вторая таблица содержит только один столбец, в котором указываются выходные сигналы для соответствующего состояния автомата.

Таблица 1

Таблица 2

Граф эквивалентного автомата Мили приведен на рис.5.

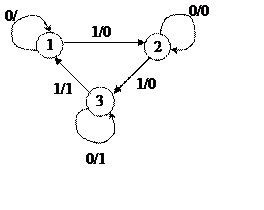
Рисунок 5

Задача 1.5. Минимизировать конечный автомат, заданный таблично таблицей переходов (табл.3) и таблицей выходов (табл.4).

Таблица 3

Таблица 4

Решение: В процессе анализа естественно оценить состояния автомата с целью минимизации их числа. Состояния автомата s_k и s_l будем считать эквивалентными, если соответствующие им строки в таблице переходов и в таблице выходов одинаковы или становятся одинаковыми при замене номеров эквивалентных состояний. В рассматриваемом примере состояния автомата 3, 4 эквивалентны. Поэтому одно из них может быть удалено. Тогда автомат будет упрощен. Например, удалим третье состояние автомата и учтем, что переходу из состояния 4 в состояние 5 в упрощенном автомате будет соответствовать переход из состояния 3 в состояние 5. Ниже на рис. 23 приведены графы исходного и упрощенного автомата Мили.

Рисунок 6

Задания для самостоятельной работы

Задание 1.1. Представить автомат Мили, граф которого приведен на рис.7, автоматом Мура. Использовать различные формы задания автомата.

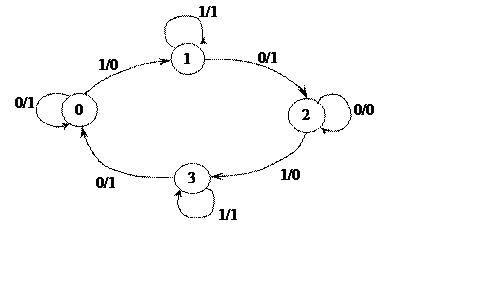Рисунок 7

Задание 1.2. Минимизировать конечный автомат, заданный таблично таблицей переходов и таблицей выходов.

Таблица переходов

Таблица выходов