Задания на практические работы по дисциплине «Моделирование систем», страница 13

где         L₁(t) – число заявок в памяти;

L₁(t) – число заявок в АОС.

Множество состояний обозначим двумя цифрами в соответствии со значениями элементов этого вектора. Данная СМО – двухфазная. Схема «гибели-размножения» для нее в допущении, что потоки забывания учебного материала и его восстановления являются простейшими,  имеет  вид, как показано на рис.43.

Для составления алгебраических уравнений Колмогорова надо вычислить l. Так как  одни сутки равны 24 часам, то l=0,008 ч^-1.

Рисунок 43

Система алгебраических уравнений Колмогорова имеет вид:

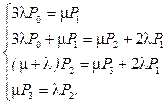
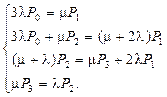
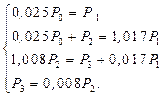
Заменим одно из уравнений уравнением нормировки:

Р₀ + Р₁ + Р₂ + Р₃ = 1.

Получим:

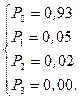
Таким образом, при нахождении марковской цепи в стационарном состоянии с вероятностью 0,93 слушатель помнит все понятия учебной дисциплины. Вероятность того, что он забудет все три понятия, практически равна нулю.

Задача 3.9. Система массового обслуживания в соответствии с классификацией Кендалла имеет вид (M/G/1).  Известны параметры потоков l=1,0 с^-1, m=2 с^-1. В соответствии с указанной записью входной поток является простейшим, а поток обслуживания является потоком общего вида. Пусть известно значение коэффициента вариации для потока обслуживания с_µ=0,5. Необходимо найти математическое ожидание времени нахождения заявки в СМО.

Решение: Для решения данной задачи воспользуемся формулами Полячека – Хинчина, имеющими вид:

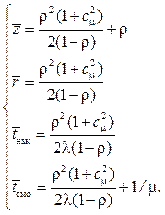
Подставляя в данные формулы известные по условию задачи значения, получим r = 0,5, с.

Задача 3.10.  Рассматриваемая СМО имеет вид (D/N/1). В данной СМО согласно приведенной записи входной поток D – детерминированный, а поток обслуживания  N – равномерный. Известны  временные характеристики для этих потоков:  c;  t_обсл = 2±1 c. Нужно найти математическое ожидание времени нахождения заявки в очереди на обслуживание .

Решение: В данной задаче, в отличие от предыдущей, входной поток не является простейшим. Поэтому ранее приведенные формулы Полячека – Хинчина использовать нельзя.  В этом случае следует рассматривать потоки общего вида и СМО, в которых сняты ограничения, как на поток обслуживания, так и на входной поток, то есть данную СМО можно представить как СМО вида   (G/G/1). Для таких СМО точных формул для вычисления характеристик таких систем не существует. Однако для случая большой загруженности СМО, когда  r »1, можно использовать приближенные формулы Полячека – Хинчина:

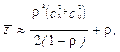
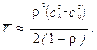
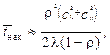
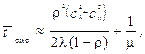
где с_l,  с_m – коэффициенты вариации для   входного потока и потока обслуживания с параметрами l и m соответственно. Чем ближе r к 1, тем формулы будут более точными. При большой загруженности системы массового обслуживания  точность вычисления имеет один порядок со значением 1/l.

Определим коэффициенты вариации для входного потока и потока  обслуживания для случайных величин X, времени между соседними заявками во входном потоке и времени обслуживания заявки в канале:

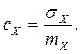
Входной поток является детерминированным. Значит, время между соседними заявками потока постоянно: s_Х=0. Следовательно: С_l=0.

Для равномерной случайной величины, времени обслуживания заявки в канале 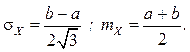  где a и b – границы области возможных значений этой случайной величины. В рассматриваемом примере  a = 1,    b = 3. Следовательно,   m_t =2 с,  s_t =0,6 с. Отсюда коэффициент вариации для потока обслуживания С_m=0,3.

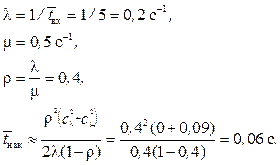
Таким образом, заявка практически не ждет своего обслуживания в очереди и при появлении сразу поступает на обслуживание.

4 СТОХАСТИЧЕСКИЕ СЕТИ

Стохастической сетью называется сеть, вершинами которой являются отдельные СМО, а дуги определяют направление потока заявок между ними. Дуги сети взвешены вероятностями переходов потоков между вершинами.

Сеть считается заданной, если заданы: интенсивность входного потока L; вектор числа каналов, входящих в каждую СМО стохастической сети – (m₁, m₂,…,m_M) , где М – число СМО, m₁ – число каналов в первой СМО,    m_М – число каналов в М-й СМО; вектор интенсивности потока обслуживания в каждой СМО – (m_1, m₂,…,m_М) или в каждом канале СМО; матрица передач P= êêp_ij êê, указывающая вероятности перехода заявок между СМО сети в процессе обслуживания.