Информатика и выч. техника \ Моделирование систем

Задания на практические работы по дисциплине «Моделирование систем», страница 6

S1 – ЭВМ неработоспособна.

S={S0, S1}.

Построим граф состояний марковского процесса (рис.13).

 


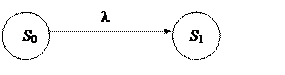Рисунок 13

Построим дифференциальные уравнения Колмогорова и дополним их уравнением нормировки:

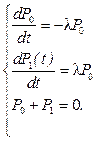
В данной системе кроме двух дифференциальных уравнений имеется уравнение нормировки. Одно из уравнений является избыточным. Для решения данной системы исключим одно из уравнений, например второе.

Получим систему уравнений.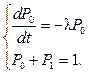

Так как первое уравнение содержит одну неизвестную, решим его. Для решения дифференциального  уравнения  нужно задаться начальными условиями. Пусть известно, что в начальный момент времени ЭВМ исправна, P0(0)=1.

Решим уравнение методом разделения переменных. Для этого обе части разделим на P0  и умножим на dt:

.

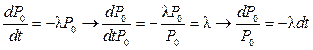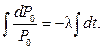
 - общее решение дифференциального уравнения. Преобразуем это выражение (избавимся от логарифма):

Найдем коэффициент  С при t=0.

P0(0)=1, Отсюда  C=1.

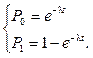
Ниже на рис.14 приведено графическое решение данной системы для случая, когда интенсивность l=0,2с-1.

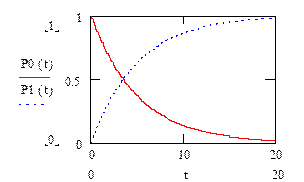
Рисунок 14

Решение данной задачи показывает, что со временем вероятность отказа ЭВМ возрастает, асимптотически приближаясь к единице.

б) Для данного случая в числе состояний по сравнению с предыдущим вариантом изменений нет: So и S1. Однако в этом случае существуют два потока: поток отказов и поток восстановлений. Поэтому граф марковской цепи имеет две, а не одну дугу (рис.15). Эти дуги помечены интенсивностями потоков l и m.

 


Рисунок 15

Система уравнений с учетом уравнения нормировки будет иметь вид:

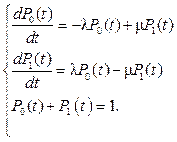
После ее решения: для начальных условий P0(0)=1, P1(0)=0  получим:

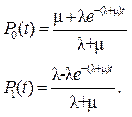
Представим решение системы в графической форме для значений параметров потоков: l=0,2 с-1; m=0,4 с-1 (рис.16).

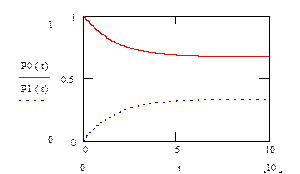
Рисунок 16

Данные графики показывают, что можно выделить переходный и установившийся (стационарный) режимы марковской цепи. Это происходит вследствие того, что данная цепь является эргодической и в ней нет поглощающих состояний.

Для стационарного режима вероятность нахождения процесса в различных состояниях не зависит от времени. Поэтому производные в левых частях дифференциальных уравнений превращаются в нуль. Вместо системы дифференциальных уравнений получаем систему алгебраических уравнений:

.

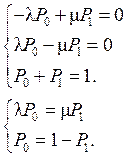
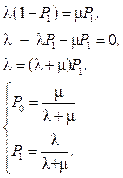в) В этом случае анализируется функционирование вычислительного комплекса, состоящего из трех ЭВМ, в котором используется схема горячего резервирования (рис.17).

 


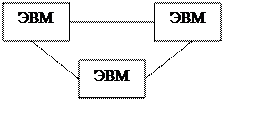Рисунок 17

Так как все ЭВМ вычислительного комплекса одинаковые, то потоки отказов в каждой ЭВМ имеет  одинаковый параметр l. Таким образом, в вычислительном комплексе существует суммарный поток отказов с числом слагаемых, равным числу исправных ЭВМ комплекса.

Марковская процесс для данного варианта задачи содержит следующие состояния:

S0 – все три ЭВМ исправны;

S1 – отказ одной ЭВМ. Так как все ЭВМ однотипны, то неважно какая из ЭВМ откажет;

S2 –отказ любых двух ЭВМ из трех;

S3 – отказ всех ЭВМ вычислительного комплекса, приводящий к отказу всего комплекса.

Граф марковской цепи состоит из четырех вершин, связанных между собой дугами. Данные дуги взвешены интенсивностями суммарных потоков отказов. Так как поток отказов простейший, то отказы идут поодиночке. Поэтому в графе связаны между собой только смежные вершины    (рис.18).

 


Рисунок 18

г) Пусть используется схема с ограниченным восстановлением. В этом случае восстанавливается только одна ЭВМ, даже если отказали несколько ЭВМ вычислительного комплекса. Нужно построить граф марковской цепи, описывающей функционирование такого вычислительного комплекса.

Ниже на рис.19 приведено решение задачи.

 


Рисунок 19

д) В отличие от предыдущего варианта предусмотрим неограниченное восстановление.

Граф марковской цепи для этого случая имеет вид, как показано на   рис.20.

 


Рисунок 20

Задания для самостоятельной работы

Скачать файл