Задания на практические работы по дисциплине «Моделирование систем», страница 7

Задание 2.1. Марковская цепь имеет вид, как показано на рис.21.

 

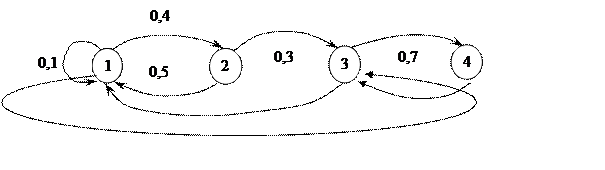Рисунок 21

Найти P(3), если известно начальное состояние марковской цепи,  P(0)=(0, 1, 0, 0).

Задание 2.2 Определить финальные вероятности нахождения дискретной марковской цепи в различных состояниях, если ее граф имеет вид, как показано на рис.22.

 

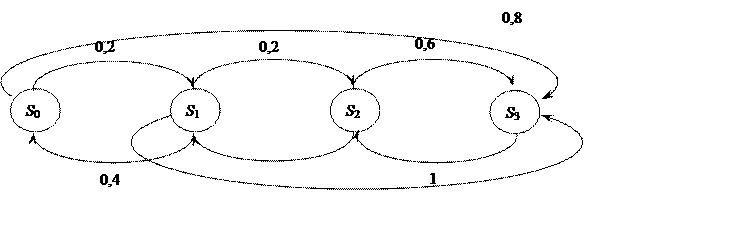
Рисунок 22

Задание 2.3 Предполагается, что во время функционирования вычислительной системы, состоящей из трех  автоматизированных рабочих мест, они могут отказывать. Причем поток отказов во всех АРМ одинаков. Система отказывает, если отказали все автоматизированные рабочие места. Известна матрица переходов марковской цепи за один шаг своего функционирования:

W =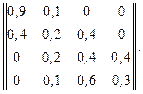

Определить вероятность того, что система работоспособна при длительном ее функционировании.

Задание 2.4 Непрерывная марковская цепь задана схемой «гибели-размножения», приведенной на рис.24. Построить дифференциальные, алгебраические уравнения и решить систему алгебраических  уравнений для l = 10 с^-1, m=20 с^-1.

 

Рисунок 23

3 МОДЕЛИ СМО

Системой массового обслуживания (СМО) называется система, состоящая из каналов для обслуживания заявок и накопителей для временного  их хранения. Она предназначена для обслуживания входного потока заявок. Процесс обслуживания заявок в системе массового обслуживания называется потоком обслуживания. В результате обслуживания заявок в СМО формируется выходной поток заявок. В него входят обслуженные заявки, а также заявки, получившие отказ. СМО предоставляет ресурс для обслуживания входного потока. Случайный характер входного потока и потока обслуживания образуют конфликт между запросами на обработку и предоставляемыми для этого ресурсами. За счет данного конфликта образуются очереди заявок на обслуживание. Поэтому теория, исследующая системы массового обслуживания, называется теорией массового обслуживания или теорией очередей.

В зависимости от характеристик входного потока и потока обслуживания, числа каналов, емкости накопителей и дисциплины постановки и обслуживания из очереди Кендаллом предложена классификация СМО. В этой классификации СМО обозначается двумя группами символов: (А/В/С): (D/E/F) ,

где:  А - входной поток заявок на обслуживание;

В - поток обслуживания заявок в системе массового обслуживания;

С - число каналов обслуживания.

Отметим, что эта тройка символов является  обязательной при задании СМО. Другие три символа, входящие во вторую группу могут не задаваться. В случае их задания данные символы означают следующее:

-  D – дисциплина постановки и обслуживания заявок в накопителе;

-  Е – емкость накопителя;

-  F – длина популяции (общее число заявок,  которые поступят на обработку в систему массового обслуживания).

Иногда в первой группе используют не три, а четыре символа, указывая также емкость накопителя.

При задании потоков указывают характер потока (см. первые два знакоместа классификации Кендалла). В этом случае используют следующие условные обозначения:

-  простейший поток - М;

-  поток Пуассона  - Р;

-  поток с гамма-распределением времени между заявками - Г;

-  поток Эрланга k-го порядка – Е_k;

-  гиперэкспоненциальный поток k-го порядка – Н_k;

-  поток общего вида  - G;

-  детерминированный поток  – D;

-  равномерный поток, т.е. поток с временем между соседними заявками, распределенным по равномерному закону – N.

В соответствии с приведенной классификацией определены стандартные классы СМО, для некоторых из которых получены математические модели, позволяющие вычислить их основные характеристики.

Задача 3.1.  Пункт обработки позволяет одновременно обслуживать три заявки. Каждый оператор пункта обслуживает только одну заявку. Среднее время обслуживания одной заявки Т=2 мин. Поток заявок является простейшим с интенсивностью потока l=0,5 мин^-1. Если при появлении очередной заявки все операторы заняты, то она получает отказ. Определить вероятность отказа – P_отк.