Использовать другие формы задания автомата.
Марковские цепи относятся к классу дискретных стохастических моделей функционирования. С их помощью описываются марковские случайные процессы с дискретным и непрерывным временем. Случайный процесс называется марковским или процессом без последействия, если для каждого момента времени вероятность любого состояния системы в будущем зависит только от состояния системы в настоящий момент и не зависит от того, каким образом система пришла в это состояние. Марковский процесс с конечным числом состояний называется марковской цепью.
Различают два основных класса марковских цепей: дискретные марковские цепи и непрерывные марковские цепи. Марковская цепь называется дискретной, если исследуемый случайный процесс является дискретным. Его аргумент принимает дискретные значения. Данный процесс имеет дискретное множество состояний. Смена состояний происходит в дискретные моменты времени – такты. При графическом задании марковской цепи она представляется ориентированным графом. Вершинами графа являются состояния марковского процесса, а дуги определяют возможные переходы процесса за один шаг дискретного времени. Дуги взвешены вероятностями такого перехода.
Марковский процесс с дискретными состояниями и непрерывным временем называется марковской цепью с непрерывным временем или непрерывной марковской цепью.
Дуги графа определяют возможные переходы случайного процесса. Непрерывная марковская цепь может быть получена из дискретной, если величина кванта времени Dt ® 0. Тогда вместо вероятности перехода за один шаг используется понятие интенсивности перехода.
Задача 2.1. Прикладная задача АСОИУ, предназначенная для обоснования варианта решения, находится в трех состояниях:
1. Решается очередной вариант задачи.
2. Анализируются полученные результаты и принимается решение.
3. Утверждается целесообразный вариант.
На каждое действие отведено примерно одинаковое время Dt = 1 мин. Сколько нужно времени для утверждения с р = 0,9, если матрица вероятностей переходов между состояниями имеет вид:
![]()
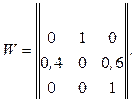
Решение: Представим процесс поддержки принятия решения как марковский
процесс с дискретным временем. В начальный момент времени t=0
процесс находится в первом состоянии, так как начинается решение задачи: ![]()
По формулам полной вероятности P(1)= P(0)W. После второго шага P(2)= P(1) W= P(0) W2. После третьего шага P(3)= P(2) W= P(0) W3 и т. д.
Р(n) = P(n - 1) W= P(0)Wn.
Таким образом, нужно найти такое значение n, чтобы Р3(n) ³ 0,9.
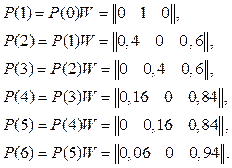
Так как каждый такт времени равен 1 мин, то с вероятностью больше чем 0, 9 задача будет решена через 6 минут.
Задача 2.2. Известно, что вычислительный комплекс отказывает в среднем через 2 часа. Какова вероятность того, что вычислительный комплекс находится в состоянии отказа через 3 часа, если его состояние проверяется 1 раз в 30 минут?
Решение: В предположении, что поток отказов является простейшим,
можно определить вероятности перехода из одного состояния в другое. Так как в
простейшем потоке математическое ожидание времени между заявками ![]() где l
- интенсивность потока отказов, то λ= 0,25 ч -1.
где l
- интенсивность потока отказов, то λ= 0,25 ч -1.
Для простейшего потока отказов, вероятность того, что вычислительный комплекс откажет за 30 мин или 0,5 часа, равна
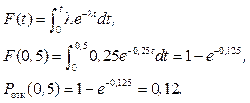
Граф марковской цепи представлен на рис.8.
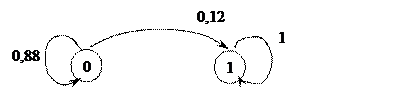 |
Рисунок 8
Построим матрицу вероятностей переходов за один шаг
![]()
Если предположить, что в начальный момент ЦВК был исправен, то ![]()
Чтобы определить вероятность отказа вычислительного комплекса через три часа, нужно вычислить соотношение:
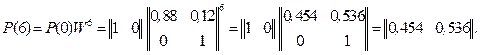
Таким образом, вычислительный комплекс откажет через три часа работы с вероятностью 0,536.
Задача 2.3. Оператор автоматизированного рабочего места АСОИУ при вводе исходных данных может обнаруживать свою ошибку набора. Если ошибка оператором не обнаружена, то информационно-поисковая система АСОИУ автоматически осуществляет синтаксический и семантический контроль набранного сообщения. Пусть все операции выполняются примерно за одно время t = 5 c. Какова вероятность того, что через 20 с начнется решение задачи, если марковская цепь имеет вид, как показано на рис.9?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.