Задания на практические работы по дисциплине «Моделирование систем», страница 14

При анализе работы стохастической  сети используют такие же  характеристики, решаются такие же задачи, что и при анализе СМО. К этим характеристикам относятся: математическое ожидание времени нахождения заявки в сети, а также во всех ее накопителях  mt_сети и mt_нак, математическое ожидание  числа заявок в сети и в накопителях m_n и m_нак соответственно.

Кроме того, используется понятие состояния сети, которое определяется вектором (n₁, … , n_M), где n_i – число заявок в i-й СМО и характеристикой Р(n₁, … , n_M) – вероятность нахождения сети в состоянии (n₁, … , n_M). Данная характеристика является наиболее полной.

Задача 4.1. Открытая стохастическая сеть состоит из трех СМО и описывается матрицей передач:

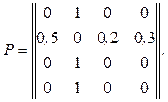
Напомним, что для открытой стохастической сети мы замыкаем ее через среду и добавляем еще одну СМО, моделирующую среду. Поэтому матрица имеет размерность 4x4. В данной матрице первая строка и первый столбец описывают поведение среды.

В приведенной матрице ее элемент р_ij  означает вероятность передачи заявки из i-й в j-ю сеть. Необходимо определить коэффициенты передач стохастической сети а_i.

Решение: Матрица передач позволяет представить стохастическую сеть, которая для рассмотренного примера приведена на рис.44.

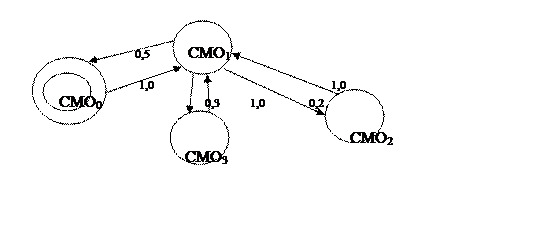Рисунок 44

Напомним, что коэффициенты передач  показывают, сколько, в среднем, раз попадает заявка в соответствующую СМО в процессе обработки. Эти коэффициенты позволяют определить интенсивности входных потоков в каждую СМО стохастической сети с помощью соотношения  

При условии стационарного режима в сети существует линейная зависимость:

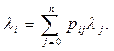
Суммирование здесь производится, начиная с нуля, так как СМО, моделирующей среду, присваивают нулевой номер. Данная зависимость позволяет построить систему алгебраических уравнений.

Построим систему алгебраических уравнений и найдем  a_i:

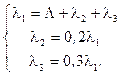
В общем случае такая система уравнений имеет ранг N, а количество неизвестных N+1, где N – число СМО в стохастической сети. Поэтому система имеет бесконечное число решений.  Выберем одну l, а именно L,  за базовую и представим другие через нее.

Подставляя в первое уравнение l₂ и l₃, из второго и третьего уравнения получим:

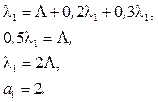
Таким образом, получаем значения коэффициентов передач:

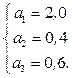
Эти значения показывают, что входной поток L перераспределяется, и СМО участвуют по-разному в обработке заявок. Наиболее загруженной является СМО₁. Поэтому именно к нему нужно предъявлять самые высокие требования по производительности.

Задача 4.2. Для условий первой задачи определить, в каком случае будет существовать стационарный режим работы сети, если интенсивность входного потока L=1 с^-1, а также известны коэффициенты передач:

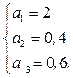
Решение: Чтобы стационарный режим  в стохастической сети мог существовать, должно выполняться неравенство  l_j / m_j ≤ 1 для одноканальных СМО сети  или l_j / m_jm_j ≤ 1 для многоканальных СМО, где m_j – число каналов в j-й СМО. В рассматриваемом примере все системы массового обслуживания являются одноканальными. Поэтому для них должно быть обеспечено выполнение требования l_j / m_j ≤ 1.

Подставляя выражения для определения коэффициентов передач, получим: a_jL/ m_j ≤ 1.

Это позволяет определить требования для максимального значения интенсивности входного потока в стохастическую сеть:

L _треб ≤  { mj / a_j}.

Отсюда можно найти требования к производительности каждой СМО для существования стационарного режима._.

.

Отсюда,  m_требj ≥а_jL.

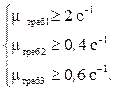
Самой нагруженной является первая СМО. К ней необходимо предъявлять самые высокие требования по производительности.

Задача 4.3 Локальная вычислительная сеть имеет четыре абонента. К ним относятся два автоматизированных рабочих места (АРМ), модуль базы данных (БД) и модуль внешних  связей (МВС). К модулю внешних связей подключены источники информации (ИИ), а также объекты управления (ОУ). Структура сети представлена на рис.45.