
Рисунок 45
Нужно построить стохастическую сеть и систему уравнений для определения значений коэффициентов передач ai .
Построим стохастическую сеть. Данная стохастическая сеть является открытой. Поэтому в состав сети дополнительно введем СМО0, моделирующую среду. Таким образом, сеть будет состоять из пяти СМО, четыре из которых будут представлять собой абоненты вычислительной сети. С учетом логики функционирования вычислительной сети оценим вероятности передач заявок при их обработке. Полученные значения вероятностей имеют оценочный характер и определены исходя из анализа протоколов взаимодействия реальных сетей. Таким образом, получим структуру, которая приведена на рис. 46.
 |
Рисунок 46
Решение: Построим систему алгебраических уравнений для определения значений коэффициентов передач:
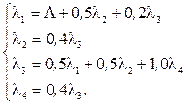
Отсюда получим:
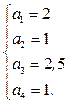
Задача 4.4 Обобщенная структура контура автоматизированной системы приведена на рис.47.
 |
Рисунок 47
Данным контуром обрабатываются данные, поступающие от источников
информации через каждые 10 секунд; ![]() . Предположим, что
входной поток является простейшим с математическим ожиданием времени между
заявками равным 10 с. Нужно определить время цикла управления
. Предположим, что
входной поток является простейшим с математическим ожиданием времени между
заявками равным 10 с. Нужно определить время цикла управления ![]() в информационной системе (математическое
ожидание времени), если задача обработки решается в ЦВК в циклическом режиме за
время
в информационной системе (математическое
ожидание времени), если задача обработки решается в ЦВК в циклическом режиме за
время ![]() Оператор утверждает машинные рекомендации
с вероятностью 0,4 (
Оператор утверждает машинные рекомендации
с вероятностью 0,4 (![]() ) или корректирует выработанные
рекомендации. После утверждения машинных рекомендаций управляющие воздействия
автоматически выдаются на потребители,
) или корректирует выработанные
рекомендации. После утверждения машинных рекомендаций управляющие воздействия
автоматически выдаются на потребители, ![]()
Решение: Построим стохастическую сеть. Граф данной сети приведен на рис.48.
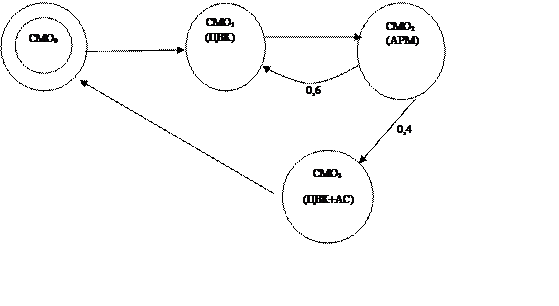 |
Рисунок 48
Составим систему алгебраических уравнений и найдем ai:
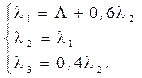
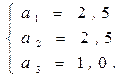
![]()
Определим
коэффициенты![]() для каждой СМО, входящей в состав
стохастической сети. С этой целью определим интенсивности входных потоков в
каждую СМО и интенсивности потоков обслуживания:
для каждой СМО, входящей в состав
стохастической сети. С этой целью определим интенсивности входных потоков в
каждую СМО и интенсивности потоков обслуживания:
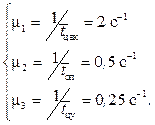
Для определения
интенсивностей входных потоков определим интенсивность входного потока в
стохастическую сеть: ![]()
Отсюда:
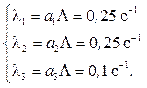

Так как для всех систем массового обслуживания ![]() ,
существуют необходимые условия для существования стационарного режима в сети.
Предположим, что такой режим существует, и определим
,
существуют необходимые условия для существования стационарного режима в сети.
Предположим, что такой режим существует, и определим ![]() ,
в предположении, что каждая СМО является простейшей, то есть относится к СМО
вида (M/M/1).
,
в предположении, что каждая СМО является простейшей, то есть относится к СМО
вида (M/M/1).
Для решения задачи будем использовать теорему Джексона, предполагающую, что при выполнении определенных условий все процессы, происходящие в отдельных СМО, являются независимыми. Стохастическая сеть может быть рассмотрена как марковская цепь, в которой состояния соответствуют стадиям обработки одной заявки в различных системах массового обслуживания. Таким образом, исследование сети сводится к исследованию всех СМО, входящих в сеть, и объединению полученных результатов. Поэтому по известным соотношениям определим временные характеристики всех СМО для данной задачи.
Воспользуемся формулой Литтла:
![]()
Подставляем zi как ![]() , получим:
, получим:
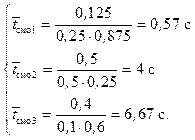
С учетом того, что заявка в каждой СМО находится ai число раз, определим:
![]()
Задания для самостоятельной работы
Задание 4.1. Определить математическое ожидание времени нахождения заявки в сети, если матрица вероятностей передач имеет вид:
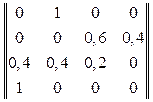 .
.
Вектор интенсивностей потока обслуживания имеет вид:
M=(10 12 10) с-1 .
Интенсивность входного потока: l0=4 с-1.
Задание 4.2. Определить вероятность того, что в сети находится ровно одна заявка, если матрица вероятностей передач имеет вид:
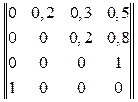 .
.
Вектор интенсивностей потока обслуживания имеет вид:
M=(20 14 12) с-1.
Интенсивность входного потока l0=6 с-1.
Задание 4.3. Определить вероятность того, что в сети не находилось ни одной заявки, если матрица вероятностей передач имеет вид:
 .
.
Вектор интенсивностей потока обслуживания имеет вид:
M=(20 10 20) с-1,
интенсивность входного потока l0=8 с-1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.