Дифференциальная оценка качества является одним из необходимых этапов комплексной оценки, кроме того, комплексные методы применяются для оценки свойств различных уровней иерархии качества, именно поэтому они получили наибольшее распространение.
Примерный алгоритм комплексного метода оценки качества представлен на рисунке 11.
Комплексную оценку качества можно рассматривать как двухэтапный процесс: первый этап – оценка простых свойств (m-го уровня); второй – оценка сложных свойств, вплоть до 0-го уровня.
Принятие любого управленческого решения сводится к выбору оптимальной альтернативы среди множества допустимых. Как правило данная цель заключается в оптимизации системы по заданному критерию, что отражается целевой функцией.
Однако в реальных условиях, при принятии управленческих решений в области технической эксплуатации, подобных целей может быть несколько, причем часто противоречивых. Так, например, чем больше капитальных ремонтов судна будет осуществлено за время его эксплуатации, тем благоприятнее это отразится на такой показатель технической эксплуатации, как коэффициент технического использования. Однако, с другой стороны, каждый такой ремонт увеличивает размер затрат, что негативно сказывается на показатель – удельные затраты на ремонт судна, который имеет отрицательную динамику.
Поэтому при выборе системы технической эксплуатации вместо «жестких» однокритериальных моделей целесообразно использовать более «гибкие» многокритериальные модели, основная идея которых заключается в «компромиссе» между различными целями, в нахождении решений, которые в какой-то мере удовлетворяли бы всем требованиям (а, следовательно, полностью не удовлетворяли бы персонально ни одной из них).
Учитывая, что к системе технической эксплуатации также применимо понятие «качество», то задача выбора оптимальной системы может быть сведена к поиску интегрального показателя качества по всем альтернативам с максимальным значением.
Постановка задачи выбора наиболее эффективной системы технической эксплуатации из нескольких альтернатив при наличии нескольких критериев (показателей), на основании нечетких множеств может быть представлена следующим образом.
Пусть задано множество возможных вариантов систем технической эксплуатации Х:
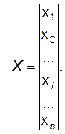
Каждый вариант характеризуется множеством абсолютных показателей качества P (см. раздел 1 данного пособия):
![]()
например P1 – удельные затраты на техническую эксплуатацию, P2 – период предельного состояния объекта и т.д.
Между каждым членом множества Х и каждым членом множества Pимеет место нечеткое отношение Kij, которое представляет собой относительный показатель качества i-го варианта системы технической эксплуатации по j-ому абсолютному показателю Pj.
Как было сказано в предыдущем разделе пособия Kij Î [0, 1]; i= 1, 2 … n; j = 1, 2 … m : если, например К11 =0, то это значит, что удельные затраты на техническую эксплуатацию объекта столь высоки, что система технической эксплуатации (вариант 1) оцененная только по этому показателю является некачественной; если К21 =1, то удельные затраты на техническую эксплуатацию объекта реализованную по варианту 2 идеально соответствует требованиям лица принимающего решения.
Таким образом данные нечеткие отношения представляют собой матрицу К размером n´m:
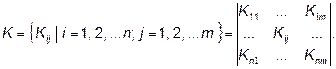
Для каждого варианта системы технической эксплуатации рассчитывается интегральный показатель качества fi. Таким образом совокупность интегральных показателей качества образуют множество F:
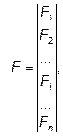
Как было сказано в разделе 3.3 данного пособия, для определения интегрального показателя качества в задачу вводится множество важностей показателей М:
![]()
где Mj – уровень важности показателя качества Pi. Уровни важности параметров качества Pj рекомендуется задавать в долях, например, если Mj = 0, то показатель Pi не оказывает влияние на выбор варианта системы технической эксплуатации, если же Мj = 1, то параметр Рi оказывает максимальное влияние на выбор.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.