Позднее нашли, что также несоизмеримы отношения длины окружности к диаметру, площади круга и квадрата, построенного на радиусе, и другие величины.
1.2. Задача приближения как одна из задач приводящих к появлению понятия иррационального числа
Пользуясь методом Ньютона (методом касательных) для нахождения приближенного решения уравнения в некоторых случаях обнаруживается, что придел последовательности рациональных чисел лежит уже не в множестве рациональных чисел.
Сущность метода Ньютона.
Будем считать, что функция f(x) удовлетворяет следующим требованиям: 1) f(x), f'(x) и f''(x) непрерывны на промежутке [a, b]; 2) значения функции на концах промежутка [a, b] имеют разные знаки; 3) обе производные f'(x) и f''(x) сохраняют каждая определенные знаки на всем промежутке [a, b], это значит, что функция строго монотонна (возрастает или убывает) на этом промежутке. Требование сохранение знака второй производной f''(x) геометрически означает, что график функции вогнутостью обращен всегда в одну сторону и не имеет перегибов. И искомый корень c изолирован на промежутке [a, b],т. е. a < c < b.
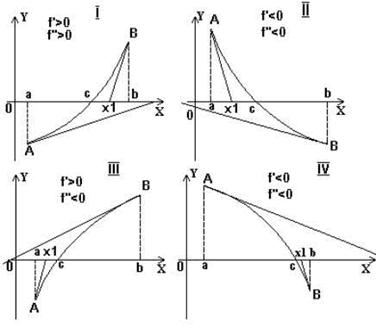
Рассмотрим уравнение касательной, проведенной в точке B с абсциссой b. Уравнение касательной в этой точке составить нетрудно, оно будет таким:
![]()
зная, что в точке пересечения с осью ОХ y = 0, найдем из уравнения значение x, получим:
![]()
Таким образом, мы получаем приближенное значение корня (формула 4)
![]() (4)
(4)
Возникает вопрос, где лежит точка x1, полученная по формуле (3). Ведь из рисунка следует, что в случаях 2 и 3 она может лежать вообще за пределами промежутка. В математическом анализе доказывается, что если значение f(b) одного знака с f''(x) - это случаи 1 и 4, то x1 лежит между корнем c и точкой b. Аналогично, если исходить из точки a, и касательную к кривой провести в точке A, то получим следующую формулу для приближенного значения корня
![]()
Также и здесь доказывается, что если f(a) и f''(a) одного знака, то x1 лежит между a и c, a < x1 < c (на рисунке это соответствует случаям 2 и 3).
Можно построить для 1-го и 4-го случаев убывающую последовательность значений xn сходящейся к c:
b > x1 > x2 > ... > xn > xn+1 > ... > c,
а для случаев 2 и 3 возрастающую последовательность значений также сходящихся к c:
a < x1 < x2 < ... < xn < xn+1 < ... < c.
Вычисление значений членов последовательности производится по следующей рекуррентной формуле:
![]()
Надо иметь ввиду, что для выбора первоначального значения x (x = a или x = b), надо установить, где знак функции f(x) совпадает со знаком f''(x).
Оценка точности приближения происходит так же, как и для случая метода хорд по значению отношения
![]()
где eps - заданная точность, а m - наименьшее значение |f'(x)| на промежутке [a, b].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.