Задачи, приводящие к появлению понятия иррационального числа. Разработка материалов для учебного модуля, страница 17

Подставляя эти соотношения друг в друга «по цепочке», представим отношение в  следующем виде:

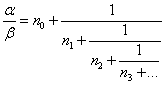
Такой вид называется цепной дробью.

Учитель: Ребята в вашем тексте вам дается новое понятие цепная дробь, мы же с вами будем работать не с цепными дробями, а с последовательностями. Это гораздо удобнее. Например, как складывать цепные дроби не понятно, а с последовательностями все очень просто.

Задание7. Постройте каждый свою величину и найдите наибольшую общую меру, пользуясь процедурой антифайресиса, запишите последовательность в виде отношений.

Обсуждение. Какие трудности были, что не понятно. У кого, сколько шагов последовательного отнятия квадратов» (у кого больше).

Учитель: А как вы считаете, какое может быть максимальное число шагов? (Почему?)

Ученик: Да, может. Потому что все равно найдется маленькая мерка, которая уложится…

Учитель: Докажи.

???

Учитель: Хорошо, пока выпишем этот вопрос на доску, и обсудим его позже еще раз.

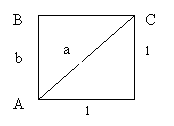Задание 8. Найдите  наибольшую общую меру у стороны и диагонали единичного квадрата. Запишите цепную дробь для этого случая.

(Задание выполняют на масштабно-координатной бумаге, инструменты: циркуль,

линейка. В ходе решения можно несколько раз поменять масштаб.)

-Примените процедуру антифайресиса к стороне ВС и диагонали АС квадрата. (Сначала самостоятельно, если не получается, то разбираем в чем трудности)

Обсуждение.

-  Ну что нашли общую меру, чему она равна? Рассказывайте, как искали?

-  Cторона ВС укладывается в диагонали АС один раз; при этом получается остаток АD. Для отнятия AD от АВ проведем DE^AC (при этом BE=AD), затем отложим EF=AD. Длина AD уложилась в AB два раза; и получился остаток AF. Остаток AF следует теперь отнимать от AD. Длина AF уложится в AD два раза и станется остаток. 

-  Хорошо, давай запишем то, что ты уже сказал, потом продолжим.

-  АС=ВС+АD=BC + r₁

AB=2AD+AF=2AD + r₂

AD=2AF+AE=2AF + r₃,

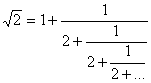
-  Посмотрите внимательно на наш чертеж (приложение), ничего не замечаете?

-  Все повторяется…

-  Теперь обратите внимание на цепную дробь.

-  Тоже все повторяется..

-  Действительно, ситуация геометрически подобна ситуации предыдущего шага. Эта же ситуация воспроизведется и на всех последующих шагах. Что это значит?

-  Это значит, что она никогда не кончится!

Действительно, процедура антифайресиса никогда не будет иметь завершения. Так мы можем продолжать до бесконечности, эта процедура не кончится.

-  Ребята, чему же тогда будет равна общая мера? И чему равно отношение стороны и диагонали квадрата?

-  У них не будет общей меры.

-  Правильно у них не будет общей меры. А величины, у которых нет наибольшей общей меры, мы будем называть несоизмеримыми. Тем самым диагональ и сторона квадрата несоизмеримы между собой, т.е. отношение  не выражается отношением целых чисел.

НО! Диагональ такоко квадрата реально существует, поэтому должно реально существовать число, выражающее длину диагонали!

-  Ну раз не выражается рациональным числом, значит, это будет число иррациональное.

Очень хорошо, молодцы. Итак, мы выяснили, что эти две величины несоизмеримы, то есть их отношение нельзя выразить рациональным числом. Значит, отношение этих величин есть иррациональное число.

Давайте теперь посмотрим на тот вопрос, который появился по ходу урока. Ну так что может процедура антифайресиса продолжаться бесконечно?

-Может

-  В чем наше сегодняшнее открытие?..