Задачи, приводящие к появлению понятия иррационального числа. Разработка материалов для учебного модуля, страница 14

ГЛАВА 3. УЧЕБНЫЙ МОДУЛЬ

3.1. Характеристика учебного модуля

Данный учебный модуль разработан для средней школы и предназначен для  8-11 классов. На практике же он был предложен учащимся 10-11 классов.

Основные цели. Расширение представлений учащихся об иррациональном числе.

Задачи.

Получить представление об истории возникновения понятия.

Описание структуры.

На первом этапе рассматривается тема «Число – отношение величин». Здесь учащиеся решают ряд задач, требующих определения отношения величины (измеряемого объекта) и мерки, причем величина  измеряется разными мерками. Дается серия аналогичных ситуаций. В результате обсуждается, что при изменении основания счета изменяется и  числовая характеристика объекта. Обсуждается, что число – это отношение величины к мерке выбранной произвольно.

Второй этап был разбит нами на ряд тем: соизмерение величин, процедура антифарейсиса, несоизмеримые величины. Задача первой темы состояла в изучении понятия соизмеримости. Занятие начиналось с обсуждения этого понятия и объяснения учителя. Затем дети перешли к решению задач на соизмерение величин, т.е. нахождение наибольшей общей меры. В ходе решения этих задач выходят на алгоритм Евклида (процедуру антифарейсиса). Это происходит следующим образом: идея процедуры антифарейсиса обсуждается на схеме «отнятия квадратов». Далее школьники записывают процедуру антифарейсиса в общем виде. Затем обсуждается, какое может быть максимальное число «отнятия квадратов», может ли оно быть бесконечным.

Учитель предлагает применить этот способ для стороны и диагонали единичного квадрата и найти наибольшую общую меру (в ходе соизмерения несколько раз увеличивается масштаб). Записывается соответствующая цепная дробь. Обсуждается эта цепная дробь, обращаем внимание на ее периодичность. Тем самым учащиеся приходят к выводу, что данные величины несоизмеримы.

Далее в ходе обсуждения выходим на то что существуют числа иной природы. Содержание беседы: 1) отношение соизмеримых величин – это рациональное число; 2) отношение несоизмеримых величин нельзя выразить рациональным числом; 3) отношение несоизмеримых величин выражается иррациональным числом.

Основные формы работы.

В ходе работы с учащимися использовались такие формы работы как фронтальная беседа, самостоятельная работа, лекция.

Фронтальная беседа применялась для того чтобы установить с учащимися обратную связь, для того чтобы привлечь учащихся к самостоятельным рассуждениям, и для того чтобы видеть понимание и непонимание учащихся. Такая форма работы как лекция использовалась в том случае, когда необходимо было донести до учащихся незнакомую им информацию.

3.2.  Проект учебного модуля

Содержание:

Тема 1. Число- отношение величин.

Тема 2.Соизмерение величин, отыскание наибольшей общей меры.

Процедура антифайресиса.

Тема 3. Несоизмеримые величины.

Тема 1. Число-отношение величин.

Задание 1. Запишите результат следующего отношения   для каждого из четырех случаев.

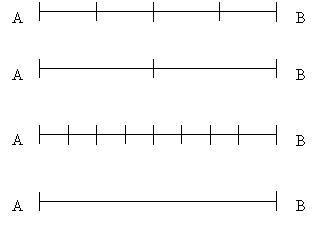
Обсуждение. Величина АВ постоянная, почему же в каждом из четырех случаев получаем разный результат?

Ученики:

-  «один» разный…