Задачи, приводящие к появлению понятия иррационального числа. Разработка материалов для учебного модуля, страница 12

Обыкновенной непрерывной дробью называется выражение вида: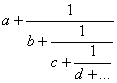

где a, b, c, d и т.д. целые положительные числа.

Таковы, например, дроби:

 ;   

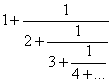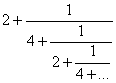
Теорема. Каждое положительное вещественное число можно однозначно представить в виде обыкновенной непрерывной дроби (цепной дроби) [].

Например: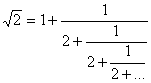            

Аппарат непрерывных дробей совершенно не допускает выполнение достаточно простых арифметических действий.

Способ представления иррационального числа как элементов геометрической фигуры

Число рассматривается как отношение величин.

Отношение двух отрезков находится с помощью алгоритма Евклида. При последовательном делении возникают два случая:

1)  последний отрезок в алгоритме Евклида будет равен нулю, а предыдущий будет общей мерой двух отрезков;

2)  деление будет продолжаться бесконечно, т.е. не будет остатка равного нулю. Общая мера будет отсутствовать.

В первом случае длины отрезков называются соизмеримыми, а их отношение можно представить в виде обыкновенной дроби и назвать – рациональным числом. Во втором случае – отношение отрезков является несоизмеримым и выражается иррациональным числом.

Например: сторона и диагональ квадрата – несоизмеримы.

2.2. Анализ введения понятия иррационального числа в существующих курсах

Для анализа я взяла следующие работы:

1)  Фихтенгольц Г. М. «Основы математического анализа»;

2)  Алимов Ш.А., Колягин Ю.М., Сидоров «Алгебра, 8 класс»;

3)  Колмогоров А.Н., Абрамов А.М., Дудницин Ю.П. и др. «Алгебра и начала анализа: учебник для 10-11 класса»;

4)  Перебаева А.А. «Понятие рационального и Иррационального числа (факультативный курс для 7-8 классов): дипломная работа».

1) Фихтенгольц Г.М. «Основы математического анализа». Глава «Вещественные числа», начинается следующим образом: «…потребности элементарной математики приводят к необходимости расширения этой числовой области.  Действительно среди рациональных чисел не существует зачастую корней даже из целых положительных (натуральных) чисел, например …». Далее идет доказательство того, что  – нерациональное число. Но одновременно с этим говорится о том, что если бы мы оставались в области одних лишь рациональных чисел, то в геометрии не все отрезки могли бы быть снабжены длинами. Это утверждение подтверждается на примере квадрата со стороной равной единице длины.

Исходя из этого, ставится и задача этой главы: расширить область рациональных чисел, присоединив к ним числа новой природы - иррациональные.

Излагая теорию иррациональных чисел, Фихтенгольц Г.М. следует Дедекинду, т.е. рассматривает иррациональное число как сечение в области рациональных чисел.

Особенность этого курса введения понятия иррационального числа в том, что Фихтенгольц излагает не историю развития понятия, а работает с готовой теорией Дедекинда. Фихтенгольц строит конструкцию, а не метод. Данная конструкция решает задачу, но не является очевидной, следовательно непосредственно для введения понятия иррационального числа использована быть не может.

2)Алимов Ш.А., Колягин Ю.М., Сидоров «Алгебра, 8 класс».