Моделирование электромеханических переходных процессов на ЭВМ: Учебное пособие (Описания лабораторных работ на ЭВМ, выполняемых студентами по дисциплине «Устойчивость узлов нагрузки»), страница 9

где DР_мех – механические потери (в лабораторных работах  DР_мех»0,01×Р_н );

с₁-коэффициент приведения цепи ротора.

Приведенное активное сопротивление фазы ротора при s=1 [6]

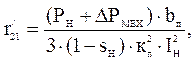
где 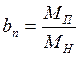- кратность пускового момента М_п двигателя; к_п - кратность пускового тока I_п двигателя, к_п=.

          Приведенное активное сопротивление фазы ротора  из-за вытеснения тока зависит от скольжения и изменяется от  до .

Поэтому для произвольного s сопротивление r^¢₂ нужно определять по формуле  [6]

       .

При выполнении заданий к лабораторным работам  нужно определять для s_н:

                                                      .                                         (4)             

          Приведенное индуктивное сопротивление рассеяния ротора  из-за вытеснения тока также зависит от скольжения и изменяется от  до _.

В [6] рекомендуется    при s>0,05 о.е. (s> 5 %)  вычислять по формуле

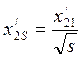                                                          ,                                                                 (5)

а в диапазоне от s»0  до s=5 % (s=0,05 о.е.) принять постоянным и равным сопротивлению  при s=0,05 о.е.

.

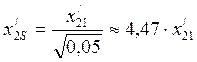При выполнении заданий к лабораторным работам №3-5 сопротивление  нужно вычислять для s_н ().

          Для определения  и  необходимо найти суммарное индуктивное сопротивление рассеяния двигателя x_s для граничных случаев. Для s =1 его можно определить (если пренебречь намагничивающим током) по формуле  [6]

                                                ,                                      (6)

 где    z_d1- полное сопротивление двигателя при неподвижном роторе.

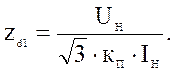                                                                                                            (7)                                                             

Для s»0 суммарное индуктивное сопротивление рассеяния двигателя [6]

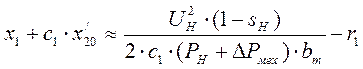                                = ,                                  (8)                            

где с₁ – коэффициент преобразования.

Решая совместно (6) и (8) , находим, что

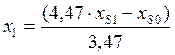                                 и       .                                     (9)    

          Однако для изучения переходных процессов более удобной является

Г-образная схема замещения (рис. 3а), в которой намагничивающая цепь вынесена к месту приложения напряжения U_d. Для перехода от Т-образной схемы к Г-об-разной необходимо вычислить коэффициент преобразования [8]    

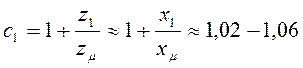                                  ,                                           (10)     

где z₁-полное сопротивление статора; z_m- полное сопротивление цепи намагничивания. В лабораторных работах с₁  следует принять равным 1,03.

          При изучении статической устойчивости асинхронной нагрузки Г-образная схема замещения обычно упрощается [2]. В схеме не учитываются: коэффициент преобразования с₁, в намагничивающей цепи – потери (r₀=0) и сопротивление х_1, а в цепи рассеяния обмоток - потери в обмотке статора (r₁=0) . В цепи намагничивания остается только индуктивное сопротивление х_m (рис. 3б).

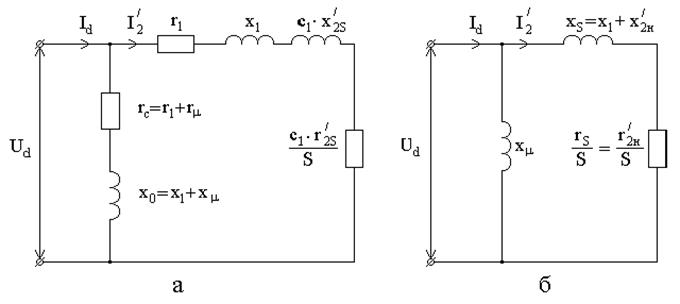
Рис. 3. Г-образная схема замещения асинхронного двигателя: а − полная;

б − упрощенная

Для цепи рассеяния обмоток (для удобства написания формул) введем обозначения x_S и r_S , где x_S равно сумме индуктивных  сопротивлений обмоток (),  а  r_S –приведенному активному сопротивлению ротора  (). Изменением сопротивлений  и  из-за вытеснения тока ротора с ростом скольжения пренебрегают и считают их постоянными (в лабораторных работах №3 и №4 они вычисляются при s_н). Эти упрощения существенно не изменяют полного сопротивления двигателя, но позволяют наглядно показать влияние скольжения s на устойчивость нагрузки (в лабораторной работе №5 при исследовании динамической устойчивости нагрузки влияние скольжения на сопротивления   и   учитывается).