Моделирование электромеханических переходных процессов на ЭВМ: Учебное пособие (Описания лабораторных работ на ЭВМ, выполняемых студентами по дисциплине «Устойчивость узлов нагрузки»), страница 18

Цель работы. Познакомиться с методикой исследования динамической устойчи-                                         вости асинхронной нагрузки на ЭВМ и определить влияние реактив-

                          ности питающей сети на допустимую длительность перерыва

                          электроснабжения и самозапуск.

          Рассмотрим динамическую устойчивость асинхронной нагрузки, под которой следует понимать способность асинхронного двигателя восстанавливать исходный режим или близкий к нему после больших возмущений. Такими возмущениями могут быть, например, короткое замыкание на питающей линии или перерыв электроснабжения, вызванный переключением двигателя на другой источник питания.

           Исследование динамической устойчивости проведем для схемы рис.10, в которой асинхронный двигатель питается через реактивное сопротивление сети x_C от генератора бесконечной мощности и вращает производственный механизм с тормозным моментом m_т. При коротком замыкании на питающей линии напряжение на двигателе снижается и уменьшается момент двигателя. На рис.17 приведены механические характеристики двигателя m_d=f(s) в доаварийном (кривая 1) и аварийном (кривая 2) режимах и механическая характеристика нагрузки m_т=const . В доаварийном режиме двигатель работал со скольжением s₀ . Произошло короткое замыкание, напряжение на двигателе уменьшилось, этому режиму соответствует характеристика 2. Так как при замыкании m_d<m_т, то двигатель начинает тормозиться, т.е. скольжение увеличивается.

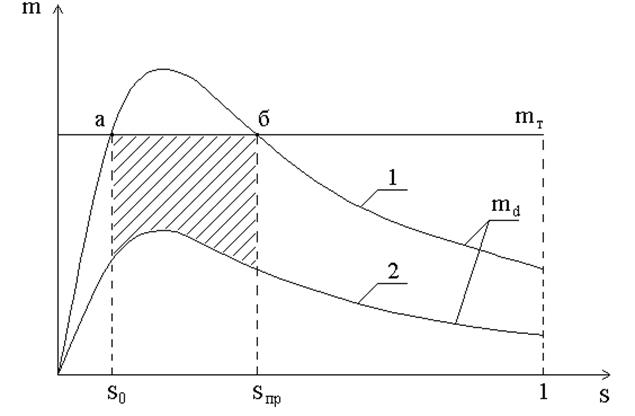
Рис. 17. Механические характеристики нагрузки и двигателя в доаварийном (кривая 1) и аварийном (кривая 2) режимах

          Для режима замыкания обычно необходимо определить предельную продолжительность замыкания, в течение которой при восстановлении напряжения двигатель может восстановить нормальную работу. Из рис. 17 следует, что если двигатель до замыкания работал со скольжением s₀ (точка а), то при замыкании оно может увеличиваться до s_пр (точка б), так как при s> s_пр после восстановления напряжения m_d< m_т и двигатель остановится.

          Еще более тяжелым режимом является перерыв электроснабжения двигателя, так как в бестоковую паузу  момент двигателя m_d становится равным нулю. В этом случае скольжение также не должно принимать значение s>s_пр  (рис.18), иначе двигатель не сможет уже прекратить торможения.

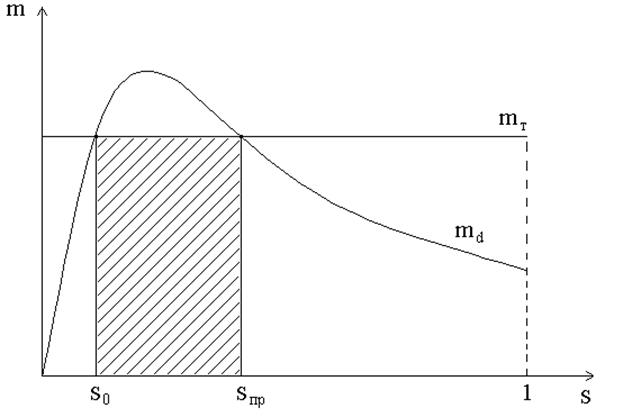
        Рис. 17. Механические характеристики нагрузки и двигателя при перерыве электроснабжения

Однако предельное время в этом случае будет значительно меньше, так как m_d=0 и  скольжение будет расти быстрее. В лабораторной работе изучается этот случай как наиболее тяжелый.

Время, необходимое для изменения скольжения от s₀  до s_пр, может быть определено интегрированием уравнения движения ротора:

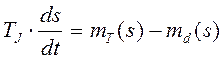                                                   ,                                               (31)

где T_J =J_пр×w₀×w_н /Р_н –постоянная инерции агрегата, приведенная к номинальной мощности двигателя; w₀ и w_н –синхронная и номинальная угловые скорости двигателя, с ^–1; Р_н – номинальная активная мощность двигателя, Вт; J_пр-приведенный момент инерции агрегата, кг×м², равный сумме момента инерции двигателя J_d и приведенного к валу двигателя момента инерции механизма J_м [5]:

,

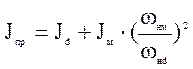где w_нм, w_нd – номинальные угловые скорости механизма и двигателя.

          Уравнение (31) можно проинтегрировать непосредственно относительно скольжения s и привести к виду

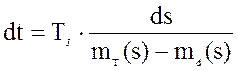                                                                                                (32)                                      

и, следовательно,

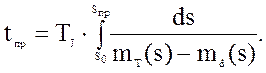                                                                                           (33) 

          Таким образом, задача определения предельной длительности возмущающего воздействия сводится к вычислению площади, ограниченной кривой:

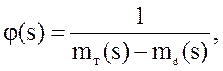
осью абсцисс и ординатами j(s₀)  и j(s_пр), которая обратно пропорциональна площади, заштрихованной на рис. 18.

          Для вычисления площади на ЭВМ моделируются механические характеристики нагрузки двух видов (см. рис. 6), построенные в относительных единицах: