Моделирование электромеханических переходных процессов на ЭВМ: Учебное пособие (Описания лабораторных работ на ЭВМ, выполняемых студентами по дисциплине «Устойчивость узлов нагрузки»), страница 19

        а) m_T = const;

б) m_T =  m_тр+(к_З – m_тр)×(1-s)^g.

Здесь введены такие же обозначения, что и в формулах (13).

          В случае перерыва электроснабжения предельное время автоматического ввода резерва в частных случаях можно найти по формуле (33) аналитическим путем. Так для m_T = const, получим

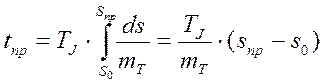                                         ,                                       (34)           

а для m_тр=0 и g=1 находим    

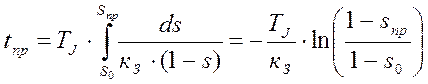                                  .                             (35)

При   m_тр¹0 и g>1 интеграл (33) не выражается через элементарные функции и его надо вычислять численными методами. Отметим, что падающая зависимость тормозного момента от скольжения приводит к увеличению s_пр и, следовательно, t_пр .

          Механическая характеристика асинхронного двигателя (в относительных единицах) при s>s_кр , как и в предыдущих лабораторных работах, строится по формуле (14). А при s<s_кр при построении механической характеристики двигателя применим более точную формулу [6]

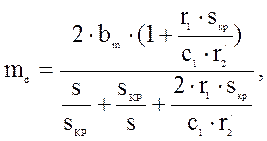                                                                                           (36)  

где s_кр – критическое скольжение, соответствующее максимальному моменту на валу двигателя [6]:

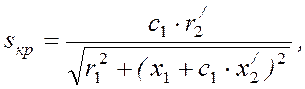                                                                                     (37)

где с₁ – коэффициент преобразования  (с₁ »1,03);  ,  ,  ,  , x_m - параметры    

Т-образной схемы замещения асинхронного двигателя (см. рис. 2, формулы (2)-(9)). Схема замещения всей цепи приведена на рис. 19.

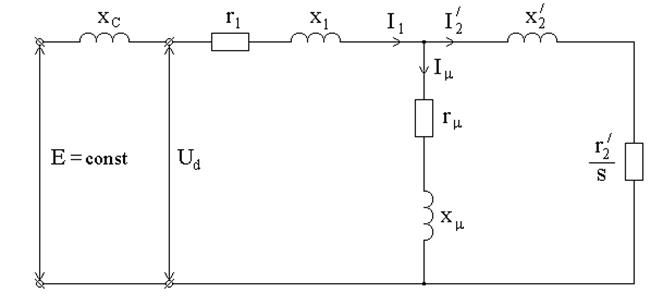
Рис. 19. Схема замещения исследуемой цепи

          Сначала в лабораторной работе изучается динамическая устойчивость асинхронной нагрузки при перерывах электроснабжения, строятся механические характеристики двигателя m_d =f (s) и нагрузки m_т=f (s)  (рис.18), определяются s₀ , s_пр и t_пр  и выводятся на экран над графиками. Механическая характеристика двигателя строится по формулам (14) и (36).

          Если x_C ¹0, то напряжение на двигателе не остается постоянным, поэтому механическая характеристика зависит от напряжения и принимает вид

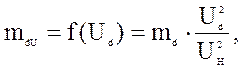
где m_d – момент двигателя, который вычисляется по формулам (14) и (36);               U_d – напряжение на двигателе, которое зависит от соотношения полных сопротивления двигателя z_d и всей цепи z [3]:

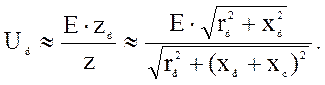
          Сопротивления двигателя (активное r_d и реактивное x_d ) в лабораторной работе вычисляются упрощенно, пренебрегаем цепью намагничивания (рис.19) и получим 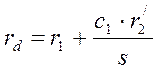                            и            .

Но при исследовании динамической устойчивости асинхронной нагрузки нельзя пренебречь вытеснением тока ротора с ростом скольжения, поэтому сопротивления  и  вычисляются по формулам (4) и (5). На рис. 20 приведена зависимость напряжения на двигателе от скольжения U_d= f (s).

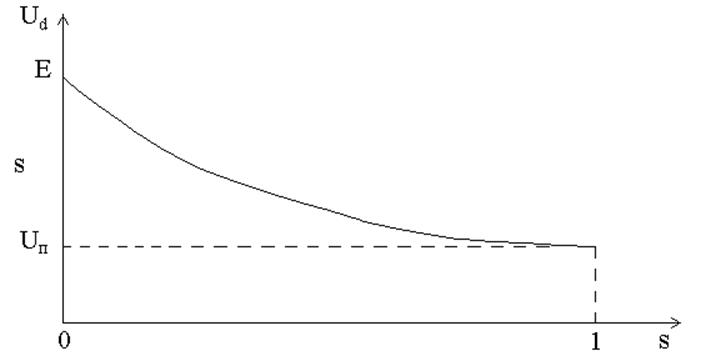
Рис. 20. Зависимость напряжения на двигателе от скольжения U_d= f (s)

          Критическое скольжение также зависит от сопротивления x_C:

 .

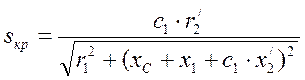          Затем исследуется динамическая устойчивость асинхронной нагрузки при самозапуске, под которым следует понимать процесс восстановления нормальной работы асинхронного двигателя после снижения напряжения на двигателе или после перерыва электроснабжения. Этот режим изучается потому, что его условия существенно отличаются от обычного пуска:

- при пуске нагрузка обычно увеличивается постепенно после разгона двигателя, а

  самозапуск происходит, как правило, при полностью включенной нагрузке;

- при пуске двигатели, питающиеся от одного источника, включаются и запускаются поэтапно, а при самозапуске все двигатели запускаются одновременно, что

приводит к увеличению тока источника и снижению напряжения на двигателях;

- при самозапуске все или часть двигателей вращаются с остаточной скоростью.

          Весь процесс расчета самозапуска можно разделить на четыре основных этапа. Рассмотрим эти этапы для случая перерыва электроснабжения. Первый этап – определение выбега двигателя, т.е. вычисление скольжения s_в, до которого происходит его увеличение в течение бестоковой паузы.