Чтобы
облегчить эту задачу, значение ![]() перед началом подбора
нужно оценить. Это можно сделать, если по правилу площадей [2] определить предельный
угол отключения короткого замыкания
перед началом подбора
нужно оценить. Это можно сделать, если по правилу площадей [2] определить предельный
угол отключения короткого замыкания ![]() , а затем подставить его
в частный случай решения дифференциального уравнения движения ротора.
, а затем подставить его
в частный случай решения дифференциального уравнения движения ротора.
Правило площадей записывается на основе закона сохранения и превращения энергии. Согласно этому закону в исследуемом случае во всех относительных перемещениях ротора сумма кинетической и потенциальной энергии остается неизменной.
В общем виде правило площадей формулируется так [2]:
![]() .
.
Для исследуемого критического случая получим (рис. 7):
![]() ,
,
где ![]() -
площадка ускорения.
-
площадка ускорения.
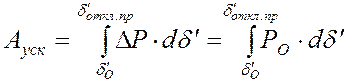 ,
,
она вычисляется от начального
угла ![]() до предельного угла отключения
до предельного угла отключения ![]() , соответствующего предельному времени
, соответствующего предельному времени ![]() ;
;
![]() -
площадка возможного торможения.
-
площадка возможного торможения.
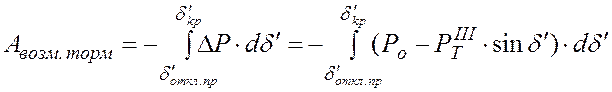 ,
,
она вычисляется от ![]() до критического значения угла
до критического значения угла ![]() , при котором
, при котором ![]() .
.
Для того
чтобы воспользоваться этим правилом, нужно построить угло-вые характеристики
мощности ![]() для трех режимов.
для трех режимов.
I. Доаварийный режим:
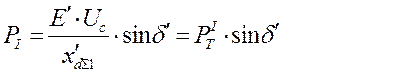 (18)
(18)
 (19)
(19)
II. Аварийный режим:
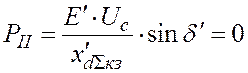 .
.
Схема замещения
электропередачи для этого случая приведена на рис. 6в, откуда следует, что при ![]()
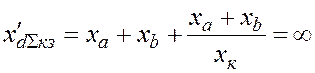
![]() .
.
III. Послеаварийный режим:
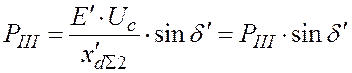 . (20)
. (20)
Послеаварийный режим принципиально возможен, если ![]() .
.
 .
(21)
.
(21)
Для предельного случая отключения короткого
замыкания площадка ускорения ![]() равна площадке
возможного торможения
равна площадке
возможного торможения ![]() (рис. 10), т.е.
(рис. 10), т.е.
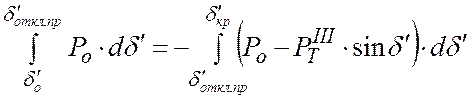 .
.
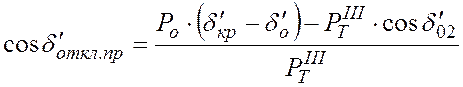 ,
(22)
,
(22)
где ![]() .
.
По углу ![]() можно оценить
предельное время отключения
можно оценить
предельное время отключения ![]() , если найти частный
случай решения дифференциального уравнения движения ротора (25). При
трехфазном коротком замыкании и отсутствии демпфирования дифференциальное
уравнение имеет вид
, если найти частный
случай решения дифференциального уравнения движения ротора (25). При
трехфазном коротком замыкании и отсутствии демпфирования дифференциальное
уравнение имеет вид
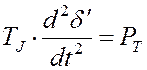 ,
,
где ![]() - постоянная инерция
ротора, о. е.;
- постоянная инерция
ротора, о. е.; ![]() - мощность турбины, о. е.
- мощность турбины, о. е.
 .
(23)
.
(23)
Из формулы (23), приняв ![]() ,
оценим предельное значение времени короткого замыкания
,
оценим предельное значение времени короткого замыкания
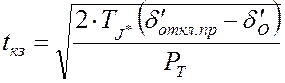 .
(24)
.
(24)
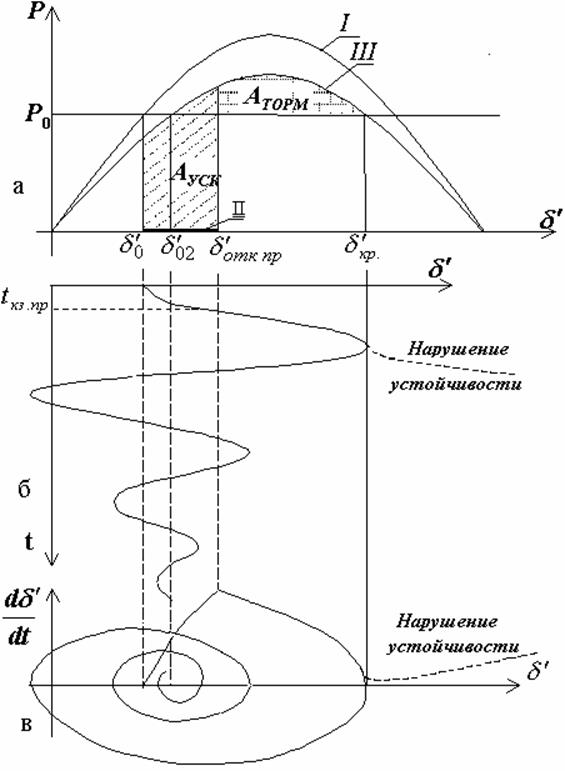
Рис. 10. Предельный случай при нарушении динамической устойчивости
системы: а – угловые
характеристики мощности ![]() для трех режимов;
для трех режимов;
б - возможные изменения угла
![]() во времени; в – характеристики ускорения
во времени; в – характеристики ускорения 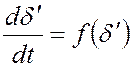 .
.
Для того чтобы по этой
формуле получить время в секундах, углы нужно подставлять в радианах, мощность ![]() в относительных единицах, а постоянную инерции
в относительных единицах, а постоянную инерции
![]() - в секундах в квадрате на радиан
- в секундах в квадрате на радиан
![]()
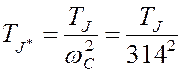 , где
, где ![]() в о. е.
в о. е.
Однако расчетное ![]() , полученное по формуле (24), меньше
, полученное по формуле (24), меньше ![]() на 5 – 15%, так как правило площадей не
учитывает демпфирование переходного процесса.
на 5 – 15%, так как правило площадей не
учитывает демпфирование переходного процесса.
Для
построения зависимости ![]() (после отключения
короткого замыкания) в лабораторной работе решается дифференциальное уравнение
движения ротора для общего случая [4]:
(после отключения
короткого замыкания) в лабораторной работе решается дифференциальное уравнение
движения ротора для общего случая [4]:
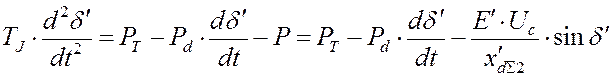 , (25)
, (25)
где ![]() -
постоянная инерции ротора;
-
постоянная инерции ротора; ![]() - мощность турбины;
- мощность турбины; ![]() - мощность генератора;
- мощность генератора; ![]() - коэффициент демпфирования, с помощью
которого учитывается действие регулятора скорости турбины или регулятора
возбуждения, реагирующих на изменение скорости
- коэффициент демпфирования, с помощью
которого учитывается действие регулятора скорости турбины или регулятора
возбуждения, реагирующих на изменение скорости  .
.
Это
уравнение решается методом Эйлера в интервале от ![]() до 5 секунд.
Для того чтобы время получилось в секундах, углы следует подставлять в
радианах, мощность – в относительных единицах, коэффициент демпфирования – в
секундах на радиан, а постоянную инерции – в секундах в квадрате на радиан.
до 5 секунд.
Для того чтобы время получилось в секундах, углы следует подставлять в
радианах, мощность – в относительных единицах, коэффициент демпфирования – в
секундах на радиан, а постоянную инерции – в секундах в квадрате на радиан.
Для времени
от 0 до ![]() полное сопротивление цепи
полное сопротивление цепи ![]() , поэтому мощность генератора
, поэтому мощность генератора ![]() и дифференциальное уравнение упрощается:
и дифференциальное уравнение упрощается:
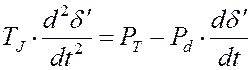
![]() .
.
На рис. 10б
показана зависимость ![]() . При
. При ![]() происходит
короткое замыкание и угол
происходит
короткое замыкание и угол ![]() начинает увеличиваться.
При
начинает увеличиваться.
При ![]() короткое замыкание отключается (в
предельном случае при
короткое замыкание отключается (в
предельном случае при ![]() и угле
и угле ![]() ),
но угол по инерции продолжает увеличиваться (в предельном случае до
),
но угол по инерции продолжает увеличиваться (в предельном случае до ![]() ), а затем уменьшается, и после ряда
колебаний устанавливается новое значение угла
), а затем уменьшается, и после ряда
колебаний устанавливается новое значение угла ![]() . Если
режим неустойчивый, то угол увеличивается неограниченно.
. Если
режим неустойчивый, то угол увеличивается неограниченно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.