Моделирование электромеханических переходных процессов на ЭВМ: Учебное пособие (Описания лабораторных работ на ЭВМ, выполняемых студентами по дисциплине «Устойчивость узлов нагрузки»), страница 2

ЛАБОРАТОРНАЯ  РАБОТА №1

ИССЛЕДОВАНИЕ СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ ЭЛЕКТРОПЕРЕДАЧИ ПРИ АВТОМАТИЧЕСКОМ РЕГУЛИРОВАНИИ ВОЗБУЖДЕНИЯ ГЕНЕРАТОРА РЕГУЛЯТОРОМ ПРОПОРЦИОНАЛЬНОГО ТИПА

Цель работы: Знакомство с переходными процессами в электрической системе при малых отклонениях параметров и отыскание значений коэффици-ентов усиления регулятора, при которых режим электрической сис-темы статически устойчив.

Статическая устойчивость электрической системы – это способность системы восстанавливать свое исходное состояние (или режим, близкий к нему) после малых возмущений режима. Исследование статической  устойчивости проведем для простейшей электрической системы (рис. 2а).

Для повышения устойчивости в электрических системах осуществляют целый ряд мероприятий, одним из которых  является применение автоматического регулирования возбуждения АРВ. Регуляторы АРВ бывают  пропорционального и сильного действия. Регуляторы пропорционального действия изменяют ток возбуждения пропорционально отклонению какого-то параметра режима.

           Пусть генератор исследуемой системы снабжен безинерционным и без зоны нечувствительности автоматическим регулятором возбуждения пропорцио-нального действия с регулированием по отклонению угла  (рис. 4), т. е.

где  - приращение э.д.с., обусловленное изменением напряжения возбудителя; - вынужденная э.д.с., пропорциональная напряжению обмотки возбуждения;

 - коэффициент усиления системы регулирования возбуждения.

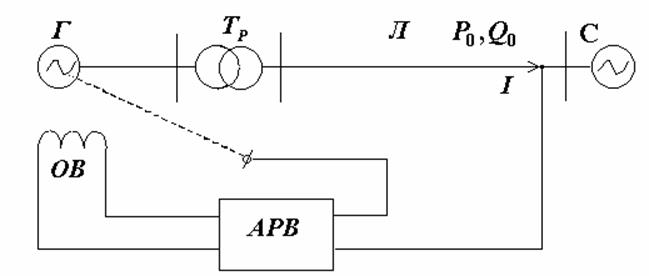
                                        Рис. 4. Исследуемая система

Если в этой системе изменяется ток генератора I, то это приводит к изменению угла  (рис. 3), тогда вступает в действие АРВ и, воздействуя на возбуждение генератора, изменяет э.д.с. и восстанавливает угол .

Однако исследуемая система будет устойчива лишь при правильной настройке АРВ, т. е. если коэффициент усиления системы регулирования возбуждения   лежит в допустимом диапазоне . Определим область устойчивой работы системы с АРВ.

Исследование статической устойчивости методом малых отклонений по существу сводится к анализу характера переходных процессов, описываемых ли-неаризованными дифференциальными уравнениями, т. е. к анализу решений этих уравнений. Если пренебречь активными сопротивлениями в цепи статора генера-тора, не учитывать апериодическую составляющую тока статора и соответствую-щую периодическую составляющую тока в обмотке возбуждения, то линеаризо-ванные дифференциальные уравнения для рассматриваемой системы представим в операторной форме в виде алгебраических уравнений [1, 2]

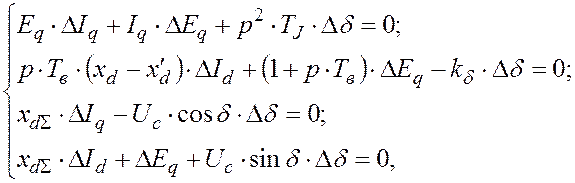                          (5)

где - отклонение параметров режима (искомые переменные системы уравнений (5); - постоянная времени обмотки возбуждения при разомкнутой обмотке статора; - постоянная инерции агрегата генератор – турбина.

          Все величины определяются в относительных единицах при единых базис-ных условиях.

Первое уравнение системы (5) является уравнением равенства моментов, второе уравнение описывает процессы в обмотке возбуждения, а третье и четвертое уравнение является уравнениями статорной цепи.

Характер решения дифференциальных уравнений определяется значениями корней характеристического уравнения, которое для системы  (5) имеет вид:

                            (6)

   где   ;

           ;

     Необходимым и достаточным условием устойчивости является отрицательность всех вещественных корней и вещественных частей комплексных корней характеристического уравнения, т. е. корни должны быть «левые». Физически это означает, что все появившиеся в момент возмущения системы отклонения параметров её режима при  стремятся к нулю.

Одним из методов, позволяющих установить отсутствие положительных вещественных корней и положительной вещественной части комплексных корней без вычисления самих корней, является метод Гурвица. Согласно этому методу все корни характеристического уравнения будут «левыми», если определители  составленные из элементов матрицы Гурвица, положительны.