Запас устойчивости для асинхронного двигателя обычно принимается равным отношению максимального момента на валу двигателя (рис. 6) к рабочему моменту [2]:
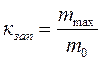 . (21)
. (21)
Рассмотрим устойчивость асинхронной нагрузки при питании ее от шин бесконечной мощности. Здесь есть некоторые отличия. Пусть от шин питается не один двигатель, а группа из нескольких разных двигателей (рис. 7б).
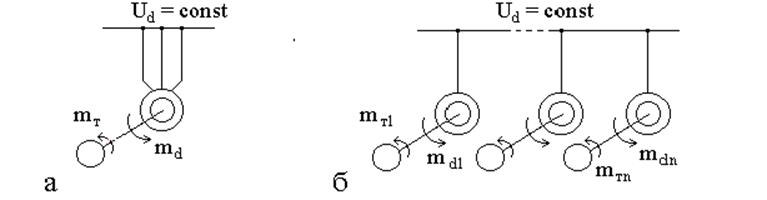
Рис. 7. Исследуемые схемы включения: а − асинхронного двигателя; б − асинхронной нагрузки
Тогда при изучении устойчивости приходится иметь дело с эквивалентным двигателем и нагрузкой с усредненными параметрами, поэтому критерий устойчивости для такого случая обычно упрощают и принимают его, как и для постоянной нагрузки (mт=const):
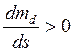 ,
(22)
,
(22)
т.е. предельным принимают скольжение sкр. Связанная с этим неточность создает некоторый дополнительный запас надежности в оценке устойчивости работы двигателей.
Для определения
области устойчивой работы асинхронной нагрузки по критерию 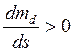 построим зависимости максимального момента
двигателя
построим зависимости максимального момента
двигателя
mmax=f (Ud) и рабочего момента m0=f (Ud) , где md=mт, от напряжения Ud (рис. 8).
Устойчивая работа асинхронной нагрузки при снижении напряжения возможна до Uкр, при котором mmax=mт. В этом случае коэффициент запаса устойчивости определяется по напряжению [3]
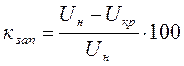 .
(23)
.
(23)
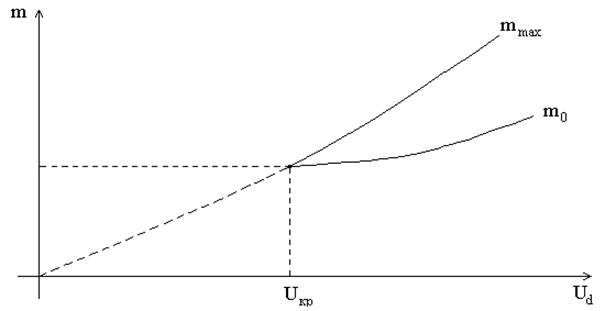
Рис. 8. Зависимости максимального момента двигателя mmax и рабочего момента m0 двигателя от напряжения на двигателе Ud
Итак,
практический критерий устойчивости асинхронной нагрузки имеет вид 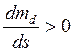 . Вычисление производной возможно, если все
двигатели нагрузки заменены одним эквивалентным. Однако определение параметров
эквивалентного двигателя часто затруднительно, что заставляет искать другие
решения, позволяющие подойти к оценке устойчивости асинхронных двигателей в
электрических системах, не выделяя их из состава комплексной нагрузки. Это
можно сделать по так называемым вторичным критериям устойчивости нагрузки.
. Вычисление производной возможно, если все
двигатели нагрузки заменены одним эквивалентным. Однако определение параметров
эквивалентного двигателя часто затруднительно, что заставляет искать другие
решения, позволяющие подойти к оценке устойчивости асинхронных двигателей в
электрических системах, не выделяя их из состава комплексной нагрузки. Это
можно сделать по так называемым вторичным критериям устойчивости нагрузки.
Рассмотрим один из таких критериев устойчивости. Для этого необходимо построить зависимости потребляемой двигателем активной Pd=f (Ud) и реактивной Q= f (Ud) мощностей от напряжения Ud (рис. 9). Эти зависимости, хотя и построены как функции от Ud , отражают определенное изменение скольжения двигателя, так как каждому значению напряжения Ud соответствует свое значение скольжения.
Потребляемая двигателем реактивная мощность в соответствии с Г-образной схемой замещения (рис. 3б) состоит из двух слагаемых:
Q = Qm + QS, (24)
где 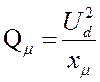 - мощность,
потребляемая ветвью намагничивания;
- мощность,
потребляемая ветвью намагничивания;
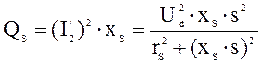 - мощность,
потребляемая ветвью рассеяния;
- мощность,
потребляемая ветвью рассеяния;
![]() -приведенный
ток цепи рассеяния.
-приведенный
ток цепи рассеяния.
Зависимости Qm=f (Ud), Qs=f (Ud) и Q=f (Ud) приведены на рис. 9.
Здесь же приведена зависимость Pd = f (Ud) , где значения электромагнитной мощности двигателя в соответствии со схемой рис. 3б определяются по формуле [3]
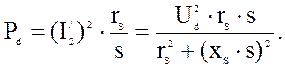 (25)
(25)
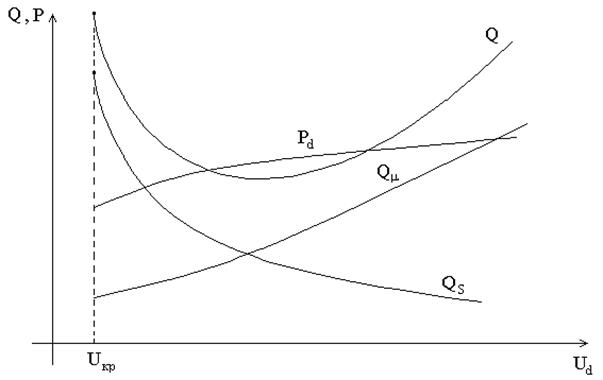
Рис. 9. Зависимости потребляемой нагрузкой активной и реактивной мощностей от напряжения на двигателе
Мощность Qs является одновременно функцией двух переменных Ud и s, поэтому при каждом новом значении Ud необходимо для условия md=mт найти новое скольжение, а затем для него вычислить Qs. Как следует из рис. 9, зависимость
Q=f(Ud) с уменьшением Ud сначала тоже уменьшается, а затем растет.
Следовательно, при 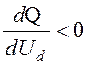 снижение Ud
приводит к росту потребляемой реактивной мощности, а значит, и к росту тока,
при питании от источника соизмеримой мощности может привести к дальнейшему
снижению напряжения на двигателе Ud.
Прогрессирующее снижение напряжения получило название лавины напряжения. При Uкр, когда
снижение Ud
приводит к росту потребляемой реактивной мощности, а значит, и к росту тока,
при питании от источника соизмеримой мощности может привести к дальнейшему
снижению напряжения на двигателе Ud.
Прогрессирующее снижение напряжения получило название лавины напряжения. При Uкр, когда 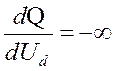 ,
происходит опрокидывание двигателя.
,
происходит опрокидывание двигателя.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.