Моделирование электромеханических переходных процессов на ЭВМ: Учебное пособие (Описания лабораторных работ на ЭВМ, выполняемых студентами по дисциплине «Устойчивость узлов нагрузки»), страница 15

-  механические характеристики двигателя для U_пред;

-  зависимости U_пред =f (g) , S_пред =f (g);

       е) основные результаты III этапа работы:

-  зависимости m _max =f (U_d) и m ₀ =f (U_d);

-  зависимости Q_m =f (U_d), Q_s =f (U_d), Q = f (U_d) и P_d =f (U_d);  

-  механическая характеристика для U_кр;

-  зависимость U_кр =f (g)  и к_зап = f (g); 

       ж) выводы по работе.

ЛАБОРАТОРНАЯ РАБОТА №4

ИССЛЕДОВАНИЕ СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ АСИНХРОННОЙ НАГРУЗКИ ПРИ ПИТАНИИ ОТ ИСТОЧНИКА СОИЗМЕРИМОЙ МОЩНОСТИ

Цель работы. Познакомиться с критериями устойчивости и методикой

                       исследования устойчивости асинхронной нагрузки на ЭВМ.

Исследования, проведенные в лабораторной работе №3, показали, что асинхронный двигатель при питании его от шин бесконечной мощности может опрокинуться лишь при снижении напряжения на шинах на 35-40 %. Однако такие снижения напряжения в установившихся режимах работы электрических систем не имеют места, и, следовательно, нужно искать другие факторы, способствующие опрокидыванию двигателей. Таким фактором является внешнее по отношению к двигателю индуктивное сопротивление системы x_C (рис. 10).

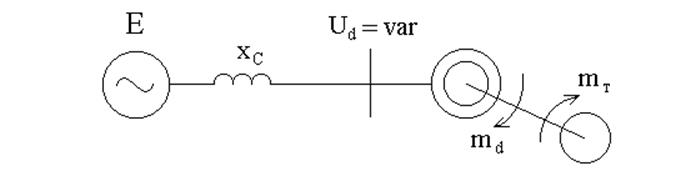
Рис. 10. Исследуемая схема включения двигателя

          В мощной электрической системе сопротивление системы x_C невелико по сравнению с сопротивлением двигателя z_d, поэтому характеристики двигателя можно строить, не считаясь с потерей напряжения на x_C. Если же речь идет о группе асинхронных двигателей, то сопротивления системы x_C и эквивалентного двигателя z_d соизмеримы, и напряжение на выводах двигателя из-за падения на x_C будет значительно ниже, чем э.д.с. генератора Е.

          Поэтому в лабораторной работе рассмотрена схема (рис.10), которая состоит из группы асинхронных двигателей, замененных эквивалентным двигателем, и эквивалентного генератора соизмеримой мощности. На рис.11 приведена схема замещения исследуемой цепи, в которой эквивалентный двигатель представлен упрощенной Г-образной схемой замещения.

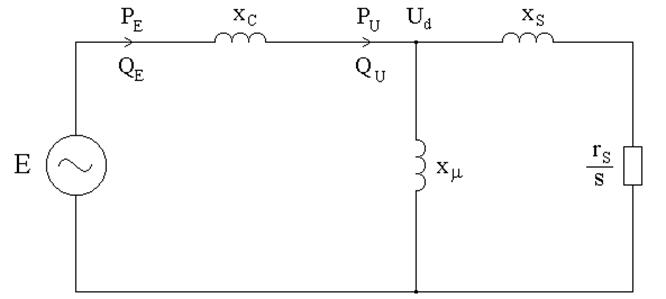
Рис. 11. Схема замещения исследуемой цепи

          Условия нарушения устойчивости (опрокидывания) эквивалентного двигателя в исследуемой схеме существенно отличаются от случая, когда двигатель питается от шин бесконечной мощности.

Во-первых, в этой схеме сопротивления x_C и z_d соизмеримы и напряжение на выводах двигателя значительно ниже, чем э.д.с. Е, из-за падения напряжения на сопротивлении x_C и уменьшается с увеличением скольжения s [2].

Во-вторых, критическое скольжение эквивалентного двигателя определяется по формуле

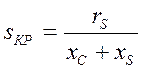
и оказывается намного меньше, чем критическое скольжение двигателя, подключенного к шинам бесконечной мощности (s_КР=r_S/x_S). Поэтому и опрокидывание двигателя в схеме рис.10 происходит при меньшем снижении напряжения.

Обычно схема замещения (рис.11) упрощается [3, 4], цепь намагничивания выносится к источнику и получаются простые расчетные формулы. Применение  ЭВМ позволяет провести исследование статической устойчивости для схемы без переноса цепи намагничивания (рис.11) . Однако при этом усложняются расчетные формулы. Напряжение на двигателе U_d при известной э.д.с. генератора Е можно найти из векторной диаграммы для исследуемой цепи (рис.12) по формуле

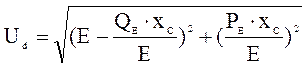                                            ,                                       (27)

где P_E  и Q_E –активная и реактивная мощности, выдаваемые генератором.

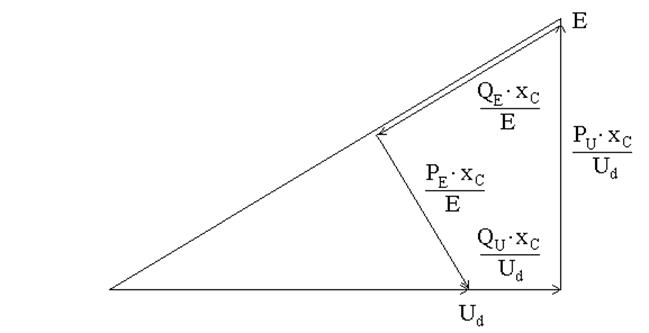
Рис. 12. Векторная диаграмма исследуемой цепи

Причем активная мощность генератора P_E  равна активной мощности, потребляемой двигателем P_U:

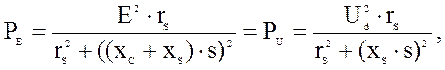
а реактивная мощность, выдаваемая генератором: Q_E=Q_U +DQ,

где Q_U –реактивная мощность, потребляемая двигателем, состоящая из мощности, потребляемой цепью намагничивания Q_m  и цепью рассеяния Q_S:

;

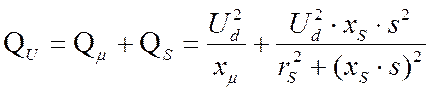DQ- потери реактивной мощности в реактивном сопротивлении сети х_С:

.

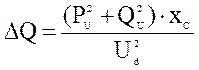Э.д.с. Е, при известном напряжении на двигателе  U_d, можно определить по формуле

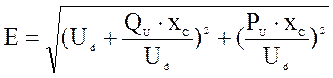                                         .                                      (28)