Для характеристического уравнения (6) определители Гурвица имеют вид:
![]() ;
;
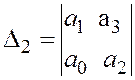 ;
;
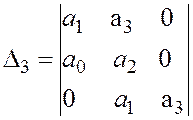 .
.
В соответствии с методом Гурвица исходный режим рассматриваемой системы статически устойчив, если выполняются условия:
![]() ; (7)
; (7)
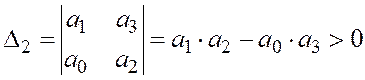 ;
(8)
;
(8)
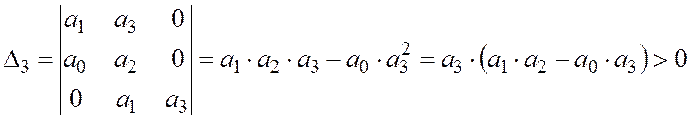 (9)
(9)
Условие (7) выполняется всегда. Из (8) и (9) следует, что при выполнении неравенства (8) неравенство (9) выполняется при условии
![]() (10)
(10)
Раскрывая (8), получим ![]() (11)
(11)
откуда
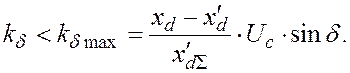 (12)
(12)
Таким
образом, неравенство (8) ограничивает сверху величину коэффици-ента усиления
регулятора ![]() , т. е. определяет верхнюю границу
значений
, т. е. определяет верхнюю границу
значений ![]() , при которых для заданного угла
, при которых для заданного угла ![]() обеспечивается статическая устойчивость
ис-ходного режима.
обеспечивается статическая устойчивость
ис-ходного режима.
Из (10) следует: ![]() ,
,
или ![]() (13)
(13)
Условие (13) определяет
минимально возможные значения ![]() , при которых ис-ходный
режим, характеризуемый углом
, при которых ис-ходный
режим, характеризуемый углом ![]() и э.д.с.
и э.д.с. ![]() , статически устойчив.
, статически устойчив.
Соотношение
(12) и (13) в функции угла ![]() определяют область
возможных значений коэффициентов
определяют область
возможных значений коэффициентов ![]() (рис. 5),
соответствующих статически устойчивым исходным режимам. Абсцисса точки
пересечения кривых
(рис. 5),
соответствующих статически устойчивым исходным режимам. Абсцисса точки
пересечения кривых ![]() и
и ![]() определяет
предельный угол
определяет
предельный угол ![]() , для которого еще возможен устойчивый
режим передачи с рассматриваемым типом регулятора возбуждения. Предельному углу
, для которого еще возможен устойчивый
режим передачи с рассматриваемым типом регулятора возбуждения. Предельному углу
![]() соответствует максимум угловой
характеристики мощнос-ти, рассчитанной при постоянстве переходной э.д.с. по
поперечной оси:
соответствует максимум угловой
характеристики мощнос-ти, рассчитанной при постоянстве переходной э.д.с. по
поперечной оси:
![]() .
.
Можно показать,
что при ![]() нарушение статической устойчивости носит
характер самораскачивания (рис. 6а), а при
нарушение статической устойчивости носит
характер самораскачивания (рис. 6а), а при ![]() -
характер «спол-зания» (апериодическая неустойчивость) (рис. 6б).
-
характер «спол-зания» (апериодическая неустойчивость) (рис. 6б).
При исследовании статической устойчивости рассматриваемой электричес-кой системы на ЭВМ систему уравнений (5) целесообразно представить в виде дифференциальных уравнений и алгебраических связей:
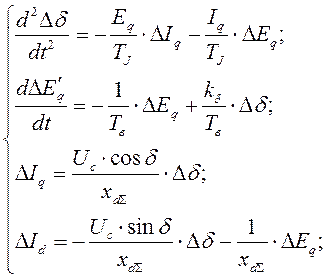 (14)
(14)
где ![]() .
.
В этом случае анализ устойчивости производится численным методом (методом Эйлера) решения системы уравнений (14). При этом малые возмущения системы можно получить автоматически из–за конечной разрядности представления чисел в ЭВМ.
Если
исходный режим, определяемый параметрами ![]() ,
, ![]() ,
, ![]() ,
, ![]() , статически устойчив, то переходной
процесс в системе, вызванный действием возмущающих сил, будит затухать и,
следовательно, отклонения параметров режима
, статически устойчив, то переходной
процесс в системе, вызванный действием возмущающих сил, будит затухать и,
следовательно, отклонения параметров режима ![]() ,
, ![]() ,
, ![]() ,
, ![]() , будут стремиться к нулю. В случае, когда исходный
режим статически неустойчив, эти отклонения будут возрастать. Поэтому в программе
предусмотрено построение четырех зависимостей
, будут стремиться к нулю. В случае, когда исходный
режим статически неустойчив, эти отклонения будут возрастать. Поэтому в программе
предусмотрено построение четырех зависимостей ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
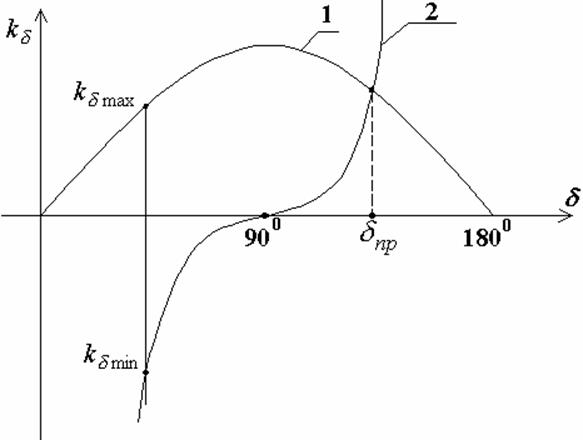
Рис. 5. Область возможных значений ![]() : 1 – кривая
: 1 – кривая ![]() ; 2 – кривая
; 2 – кривая
![]() ;
;
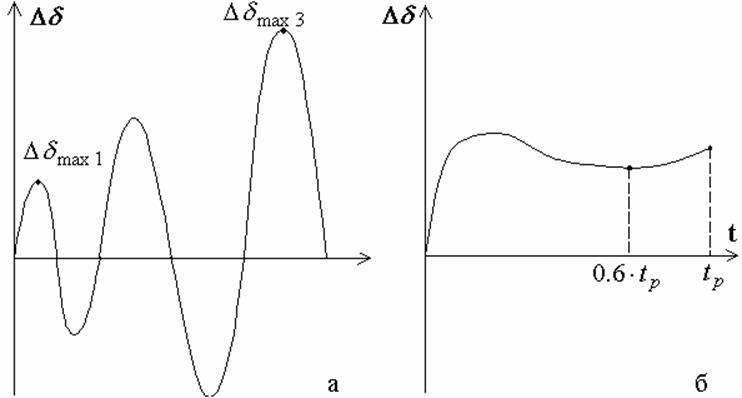
Рис. 6. Неустойчивые режимы системы: а – самораскачивание; б – «сползание»
По этим
зависимостям подбираются коэффициенты регулирования АРВ. Для более точного
определения границы (рис. 5) устойчивого режима ![]() од-новременно
с графиком на экран выводятся значения первого и третьего макси-мумов
зависимости (рис. 6а), по которым определяется затухает или раскачивается
зависимость и на сколько процентов. За границу принимается такое значение коэффициента,
при котором все зависимости отличаются от синусоиды не более чем на 1 – 2 %
(раскачивание - не более 1%, затухание – не более 2%).
од-новременно
с графиком на экран выводятся значения первого и третьего макси-мумов
зависимости (рис. 6а), по которым определяется затухает или раскачивается
зависимость и на сколько процентов. За границу принимается такое значение коэффициента,
при котором все зависимости отличаются от синусоиды не более чем на 1 – 2 %
(раскачивание - не более 1%, затухание – не более 2%).
Для более
точного определения нижней границы (рис. 5) устойчивого режи-ма ![]() одновременно с графиком на экран выводятся
значения функции для
одновременно с графиком на экран выводятся
значения функции для ![]() и
и ![]() (рис.5б),
где
(рис.5б),
где ![]() - время расчета. За границу принимается
такое значение коэффициента, при котором у всех зависимостей затухание или нарастание
приращений в этом диапазоне не превышает 5%.
- время расчета. За границу принимается
такое значение коэффициента, при котором у всех зависимостей затухание или нарастание
приращений в этом диапазоне не превышает 5%.
Общие исходные данные
![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
; ![]()
Варианты задачи
Таблица 1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.