ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального
образования
«Санкт-Петербургский государственный электротехнический университет
“ЛЭТИ” имени В.И.Ульянова (Ленина)»
(СПбГЭТУ)
-------------------------------------------------------------------------------------------------------
Методические указания
к практическим занятиям по дисциплине
«Интегрированные радионавигационные системы»
Санкт-Петербург
2012
УДК 621.391
Методические указания к практическим занятиям по дисциплине
«Интегрированные радионавигационные системы»/ Сост.: А.И.Соколов, Ю.С.Юрченко; СПбГЭТУ. – С.-Пб., 2012 – 26с.
Приведено описание 7-ти работ практического цикла дисциплины «Интегрированные радионавигационные системы». Содержатся сведения о принципах построения моделей радиотехнических систем навигации и управления и порядке их исследования в среде визуального моделирования «MatLab/Simulink». Основное внимание уделено анализу помехоустойчивости элементов радиотехнических систем. Предназначено для студентов радиотехнических специальностей.
Утверждено редакционно-методическим советом университета в качестве методических указаний
Введение
Представленные в данном методическом пособии работы обеспечивают проведение практических занятий для поддержки основных разделов дисциплины «Интегрированные радионавигационные системы». При этом основное внимание в практическом цикле уделено моделированию элементов радиотехнических систем, обеспечивающих оценку параметров радиосигналов и координат объектов. Кроме того, рассматриваются типовые траектории движения объектов.
При первом знакомстве со средой визуального моделирования «Simulink» рекомендуется лабораторный цикл начинать с выполнения первой работы, описание которой содержит подробные методические указания по составлению схемы моделирования и обработке результатов исследований. Содержание остальных работ логически связано, поэтому рекомендуется выполнять их в указанной последовательности.
Для анализа моделируемых систем применяются методы теории автоматического регулирования, известные студентам из дисциплины «Основы автоматики и САУ». Весьма полезным для студентов окажется умение выполнять вычисления в среде «MatLab» (не только в режиме прямых вычислений, но и с помощью программы; приведены примеры составления программ). Приступая к выполнению новой работы, рекомендуется тщательно проверить параметры моделирования или обновить исходный файл моделирования, так как внесенные в модель, в процессе выполнения работы другими студентами, изменения могут затруднить проведение исследований.
Практическое занятие №1
Исследование экспоненциально-коррелированного процесса
Цель работы – исследование экспоненциально-коррелированного процесса, который широко используется при моделировании радиосистем навигации и управления в случае математического представления медленно изменяющихся случайных величин. Дополнительно решается задача знакомства студентов с методами моделирования в среде «Simulink» и предварительной подготовки к выполнению более сложных заданий.
1.1. Основные теоретические сведения
Экспоненциально-коррелированный процесс можно
получить, подавая на вход апериодического звена (например, интегрирующей RC-цепи)
белый шум ![]() . В этом случае для выходного процесса
. В этом случае для выходного процесса ![]() можно
составить дифференциальное уравнение:
можно
составить дифференциальное уравнение:
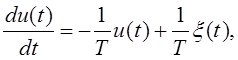 (1)
(1)
где T – постоянная времени апериодического звена (для интегрирующей RC-цепи T=RC).
Для нахождения автокорреляционной функции такого
процесса целесообразно задачу решать во временной области, поскольку такой путь
приводит к более общему результату, учитывающему нестационарные явления в апериодическом
звене. Процесс ![]() является
решением дифференциального линейного уравнения с начальным условием u(0):
является
решением дифференциального линейного уравнения с начальным условием u(0):
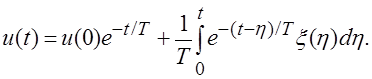 (2)
(2)
В установившемся режиме (при ![]() ) первым
слагаемым в (2) можно пренебречь и
) первым
слагаемым в (2) можно пренебречь и ![]() равно
равно
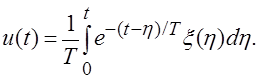
Автокорреляционная функция ![]() находится путем применения оператора усреднения к
произведению процесса
находится путем применения оператора усреднения к
произведению процесса ![]() на
сдвинутую во времени копию
на
сдвинутую во времени копию ![]() :
:
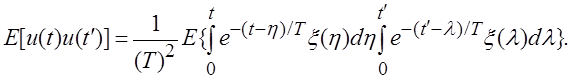
Переставляя операторы усреднения и интегрирования, получим
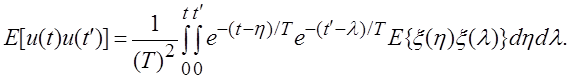
Для белого ( δ-коррелированного) шума 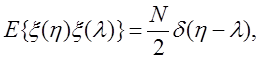 где N – спектральная плотность мощности
где N – спектральная плотность мощности ![]() .
Следовательно, с учетом фильтрующих свойств δ-функции, получаем
.
Следовательно, с учетом фильтрующих свойств δ-функции, получаем
![]()
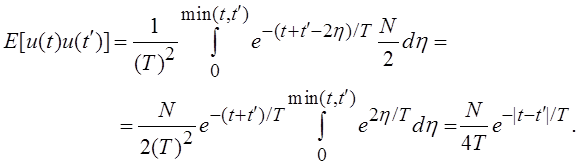
Вид автокорреляционной функция определяет название
рассматриваемого случайного процесса. Очевидно, дисперсия процесса ![]() в
установившемся режиме равна
в
установившемся режиме равна ![]() или, при введении
понятия эквивалентной 2-сторонней спектральной плотности мощности
или, при введении
понятия эквивалентной 2-сторонней спектральной плотности мощности ![]() ,
равна
,
равна ![]() .
.
При переходе от описания процесса в непрерывном
времени ![]() к описанию процесса в дискретном времени
к описанию процесса в дискретном времени ![]() вместо дифференциального уравнения используется
разностное уравнение простейшего дискретного эквивалента апериодического звена.
Решение дифференциального уравнения (1) рассматривается на интервале временной
дискретизации
вместо дифференциального уравнения используется
разностное уравнение простейшего дискретного эквивалента апериодического звена.
Решение дифференциального уравнения (1) рассматривается на интервале временной
дискретизации ![]() , при этом случайный процесс
, при этом случайный процесс ![]() описывается
уравнением
описывается
уравнением
![]() (3)
(3)
где
![]() ;
; 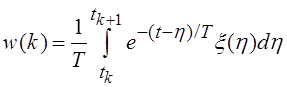 – дискретный белый шум с нулевым средним и дисперсией
– дискретный белый шум с нулевым средним и дисперсией ![]() .
.
Дисперсия шума ![]() может быть найдена непосредственно:
может быть найдена непосредственно:
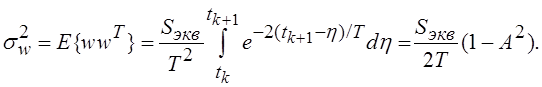
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.