Интегрированные радионавигационные системы: Методические указания к практическим занятиям, страница 6

Разностным уравнениям (5)-(7) соответствует схема, представленная на рис.5. Цифровой дальномер содержит дискретный интегратор, образуемый контуром из элемента задержки  и цепи обратной связи с сумматором. Для моделирования отсчета дальности  также используется дискретный интегратор, на вход которого поступает значение приращения дальности . Погрешность измерения моделируется случайной величиной .

Формирующий фильтр формально содержит 2 интегратора (для формирования постоянного приращения дальности  также нужен интегратор), поэтому дисперсионное уравнение дальномера имеет 2-й порядок и описывает поведение корреляционной матрицы вида: 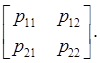 Нас интересует элемент , характеризующий ошибки дальномера. Решение дисперсионного уравнения дальномера с одним интегратором и произвольным коэффициентом усиления   для выбранной модели воздействия приводит к результату:

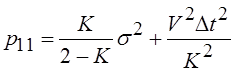,                                              (8)

где   - дисперсия ошибки дальномера в режиме экстраполяции.

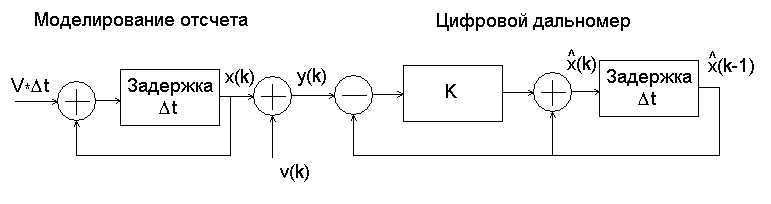
Рис.5

Минимизация  относительно   требует решения уравнения:

.

Это решение определяется выражением:

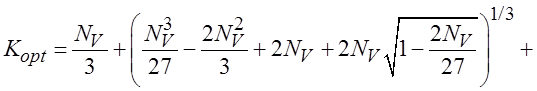
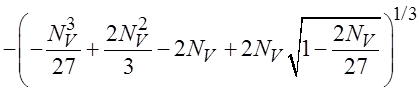,                               (9)

где 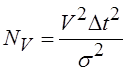,  – скорость изменения дальности,  – дисперсия шума  в измерениях дальности.

В случае выполнения условия , точностные характеристики дискретной (цифровой) и непрерывной систем практически одинаковы и можно использовать более простой способ вычисления :

.

3.2. Описание метода моделирования

Моделирование цифрового дальномера выполняется с помощью пакета «Simulink». Схема моделирования показана на рис.6 (файл для моделирования: «Lab_3_Sl1.mdl»). Приращение дальности  в этой схеме формируется блоком «Constant». Таким образом, дальность изменяется во времени с постоянной скоростью. Погрешность измерения моделируется блоком «Random Number».

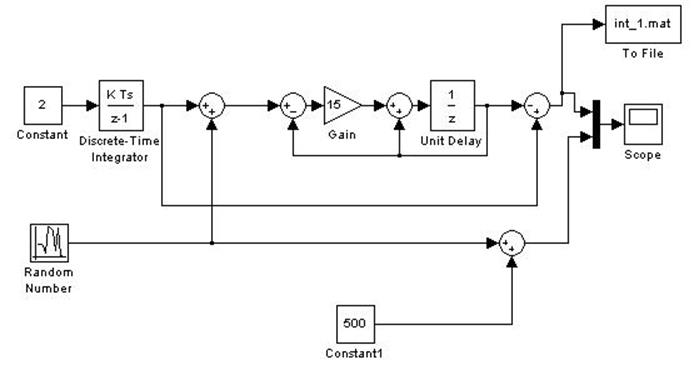
Рис.6

          Отсчет дальности суммируется вместе с погрешностью измерений и поступает на вход вычитающего устройства дальномера. Коэффициент усиления  воспроизводится блоком «Gain», цепь задержки – «Unit Delay». Разность между точным значением дальности  и оценкой дальности  на выходе дальномера (т.е. ошибка экстраполяции) поступает на запись в файл (элемент «To File») и в осциллограф «Scope» (для визуального разделения процессов с помощью осциллографа «Scope» к погрешности измерений добавляется постоянная составляющая с выхода блока «Constant1»; величину этой составляющей следует выбрать, исходя из удобства наблюдения 2-х случайных процессов).

          Параметры моделирования, как и ранее, устанавливаются в разделе меню «Simulation/Configuration parameters» (Type: «Fixed step», Solver: «discrete», параметр «Simulation time/Stop time» задается равным 5000). Для начала моделирования дается команда «Simulation/Start».

Результаты моделирования наблюдаются в виде осциллограммы, а также передаются в среду «MatLab» для последующей обработки. С этой целью формируется файл с ошибками фильтра er_1 (идентификатор файла может быть другим). Файл содержит матрицу, в которой первая строка состоит из отсчетов времени t, а вторая содержит ошибки er. Для выделения строки ошибок er и определения среднего значения mean(er), дисперсии var(er) и суммарной ошибки mean(er)^2+var(er) используются операторы:

er=[0 1]*er_1; [mean(er)  var(er) mean(er)^2+var(er)].

3.3. Задание по работе

          1. Выбрать значение приращения дальности  и дисперсию  случайного шума  в соответствии с данными Табл. 2 (два набора исходных данных соответствуют ситуациям, когда условие  выполняется и не выполняется). В среде MatLab построить зависимость  от  (вариант программы приведен ниже).

%Оптимизация параметров дальномера с 1 интегратором

clear;

Disp=36000;

DV=40;

for i=1:10;

    K=i/10;

    p=Disp*K/(2-K)+DV*DV/K/K;  % Выражение (8)

    x(i)=K;

    p11(i)=p;

end;

plot(x,p11)