Интегрированные радионавигационные системы: Методические указания к практическим занятиям, страница 7

          2. Установить параметры моделирования и построить экспериментальную зависимость дисперсии суммарной ошибки  при изменении  с шагом 0,1 вблизи минимума построенной в п.1 кривой. На осциллограммах обратить внимание на зависимость сглаживающих свойств дальномера и смещения ошибки от коэффициента усиления . Более точно (с погрешностью до величины 0,01) экспериментально определить положение минимума.

  3. Рассчитать значения  и  (по точной и приближенной формулам;

 замечание: выражение (9) для последнего слагаемого записано так, чтобы в среде MatLab не возникало вычислительных проблем). Сопоставить значение  , полученное по точной формуле с построенной зависимостью  от   с помощью приведенной выше программы. Для этого изменить 2 строки программы: i=1:1000; K=i/1000; запустить программу, вывести на экран монитора массив p11 и по минимуму определить оптимальный коэффициент.

          4. Результаты теоретического расчета сопоставить с экспериментальными данными (для коэффициента усиления и дисперсии ошибки дальномера).

          5. Увеличить время моделирования до 50000 и уточнить результаты моделирования вблизи минимума.

                                          Табл.2. Варианты заданий

3.4. Содержание отчета

1. Схема моделирования.

2. Характерные осциллограммы процессов  и .

3. Результаты теоретического расчета (точное и приближенное значения

коэффициента усиления , значение , минимальное значение ).

4. Теоретическая и экспериментальная зависимость среднего квадрата

ошибки дальномера от коэффициента усиления .

5. Результаты экспериментального оценивания оптимального коэффици-

ента усиления  и минимальной дисперсии ошибки .

6. Формулировка задач проведенного исследования и выводы по полу-

ченным результатам.

3.5. Контрольные вопросы

1. Объяснить рост суммарной ошибки при малых значениях .

2. Объяснить причину роста суммарной ошибки при увеличении .

3. При каких условиях можно использовать приближенную формулу расчета коэффициента усиления?

4. При каком условии экспериментальное значение суммарной ошибки приближается к расчетному значению?

5. Объяснить поведение оценки дальности  при пропадании радиосигнала (выход вычитающего элемента на входе дальномера равен нулю).

6. Как выбрать значение коэффициента усиления  при =0?

Практическое занятие  №4

Оптимизация параметров цифрового следящего измерителя

 с 2-мя интеграторами

Цель работы – исследование точности и параметрическая оптимизация следящего измерителя с 2-мя интеграторами методом моделирования, а также оценка его сглаживающих свойств.

4.1. Основные теоретические сведения

Маневрирование объектов вызывает необходимость повышения порядка астатизма следящих измерителей координат. При наличии ускорения в изменении координат объекта в состав систем навигации и радиоуправления включают измерители координат с 2-мя интеграторами. Если анализ дискретной следящей системы с 1-м интегратором в стационарном режиме работы требует решения алгебраического уравнения 3-й степени (см. разд.3.1), то анализ           дискретной следящей системы с 2-мя интеграторами существенно сложнее. По этой причине часто применяют численные методы анализа и оптимизации таких систем, в том числе – метод моделирования. С целью упрощения решения такой задачи в качестве начального приближения используют результаты анализа непрерывного аналога следящей системы.

В нашем случае таким аналогом является система, имеющая в разомкнутом состоянии передаточную функцию:

,

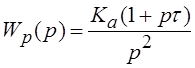где  и  - параметры непрерывной системы.