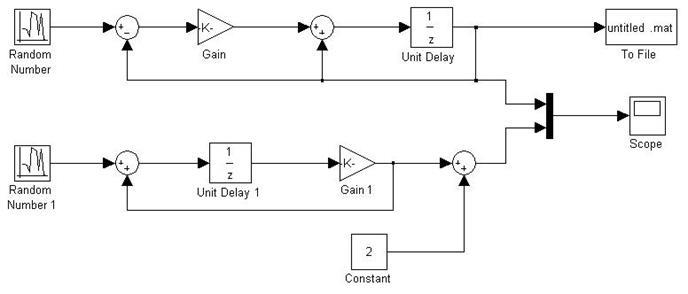
Другие предметы \ Интегрированные радионавигационные системы

Интегрированные радионавигационные системы: Методические указания к практическим занятиям, страница 5

Рис.4.

          Параметры моделирования, как и ранее, устанавливаются в разделе меню «Simulation/Configuration parameters» (Type: «Fixed step», Solver: «discrete», параметр «Simulation time/Stop time» задается достаточно большим, например, равным 100000). Для начала моделирования дается команда «Simulation/Start».

2.3. Задание по работе

          1. Выбрать значение постоянной времени в соответствии с данными Табл.1 (значение ). При задании дисперсии шума в элементе «Random Number»  учесть соотношение   (значение  равно 1). При задании дисперсии шума в элементе «Random Number 1»  учесть соотношение 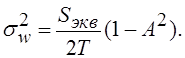 Посмотреть процессы с помощью осциллографа.

          2. Увеличить значение постоянной времени на порядок, затем на 2 порядка, фиксируя результаты моделирования с помощью осциллографа.

          3. С использованием блока «To File» для 1-й модели вычислить автокорреляционную функцию и спектральную плотность мощности (пример программы приведен ниже).

%Экспоненциально-коррелированный процесс 2а

N=100000;

proc=[0 1]*ans;

ac=xcov(proc)/N;

F=fft(ac);  % Преобразование Фурье

SPM=F.*conj(F)/N;  % Поэлементное умножение на компл.сопряж.величину

M1=length(SPM);   % Длина массива

t=1:1:M1;

plot(t,SPM)

    4. С использованием блока «To File» для 1-й модели оценить среднеквадратичное значение процессов с разными постоянными времени (использовать приближенный и точный способы; пример программы приведен ниже).

%Экспоненциально-коррелированный процесс 2б

proc=[0 1]*ans;

Max=max(proc);

Min=min(proc);

cko1=(Max-Min)/6;

cko2=std(proc); % или cko2=sqrt(cov(proc));

Результаты приближенного оценивания среднеквадратичных значений процессов сопоставить с осциллограммами этих процессов.

2.4. Содержание отчета

          1. Схема моделирования.

          2. Осциллограммы случайных процессов.

          3. Параметры моделирования для всех значений .

          4. Преобразования Фурье для всех значений .

          5. Результаты экспериментального оценивания среднеквадратичных значений случайных процессов.

          6. Формулировка задач проведенного исследования и выводы по

результатам эксперимента.

2.5. Контрольные вопросы

          1. Указать достоинства и недостатки 2-х вариантов моделирования экспоненциально-коррелированного случайного процесса.

          2. Почему обе модели формируют одинаковый случайный процесс? Как повлияет на процессы изменение числа «Initial seed» в одном из датчиков случайных чисел?

          3. Записать дисперсионное уравнение дискретной следящей системы и найти его стационарное решение.

          4. Как влияют спектральная плотность мощности входного случайного процесса и постоянная времени на дисперсию моделируемого процесса?

          5. Как можно приближенно оценить среднеквадратичное значение случайного процесса по его осциллограмме?

          6. Какое преобразование связывает автокорреляционную функцию и спектральную плотность мощности случайного процесса?

Практическое занятие  №3

Исследование цифрового дальномера с одним интегратором

Цель работы – исследование методом моделирования помехоустойчивости цифрового следящего дальномера, который широко используется в системах радиоуправления.

3.1. Основные теоретические сведения

Алгоритм работы цифрового дальномера, представляющего собой следящую систему с одним интегратором, можно описать разностным уравнением

,                    (5)

где – оценка дальности в -й момент времени,  – коэффициент усиления,  – измерение дальности, содержащее истинное значение дальности  и случайную ошибку :

.                                            (6)

При моделировании предполагается, что дальность изменяется во времени со скоростью  в соответствии с уравнением

,                                        (7)

где  – интервал временной дискретизации, определяемый периодом измерительного процесса .

Коэффициент усиления  выбирается таким образом, чтобы минимизировать ошибку слежения, которая состоит из флуктуационной и динамической (в данном случае – скоростной) составляющих.

Скачать файл