Проверить соответствие полученной дисперсии (пик графика) результатам теоретического расчета. При расчете автокорреляционной функции суммируется N отсчетов, поэтому при экспериментальном определении дисперсии максимальное значение на графике следует разделить на N.
3. Повторить эксперимент по п.2 для N=100000. Сравнить полученное значение дисперсии со случаем N=1000 и результатом теоретического расчета.
4. Выполнить моделирование по пп.1,2 и 3 для меньшего
значения 
. Сопоставив результаты моделирования, дать
рекомендации относительно выбора времени моделирования в зависимости от
величины постоянной времени и требуемой точности эксперимента.
Табл.1. Варианты заданий
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
|
Т1 |
10 |
20 |
30 |
40 |
50 |
60 |
|
Т2 |
5 |
10 |
15 |
20 |
25 |
30 |
|
|
100 |
400 |
900 |
1600 |
2500 |
3600 |
1.4. Содержание отчета
1. Схема моделирования.
2. Осциллограммы случайных процессов.
3.
Результаты теоретических расчетов
(для 2-х значений ).
4. Результаты экспериментального оценивания дисперсий процесса.
5. Вид автокорреляционной функции: аналитический (теоретический) и
графический (построенный экспериментально).
6. Формулировка задач проведенного исследования и выводы по
результатам эксперимента.
1.5. Контрольные вопросы
1. Как влияет выбор числа N на вид автокорреляционной функции
процесса?
2. В каких случаях требуется выполнять настройку числа «Initial seed» в
датчике случайных чисел?
3. Почему экспериментальное значение дисперсии случайного процесса
при моделировании зависит от значения числа N?
4. Почему экспериментальное значение дисперсии случайного процесса
при моделировании зависит от параметра T?
5. Указать способ нахождения автокорреляционной функции случайного
процесса в частотной области и сравнить его со способом, описанным в разд.1.1.
6.
Какую операцию выполняет алгоритм
(см. рис.1) при 
=1?
Практическое занятие №2
Моделирование экспоненциально-коррелированного процесса с помощью дискретной следящей системы
Цель работы – исследование альтернативного варианта моделирования экспоненциально-коррелированного процесса.
2.1. Основные теоретические сведения
Рассмотренный
в 1-м задании алгоритм формирования дискретного экспоненциально-коррелированного
процесса (3) чрезвычайно прост, но обладает существенным недостатком. Изменение
постоянной времени требует установки 2-х параметров модели: 
и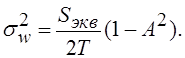 
Хорошо известно, что передаточная функция непрерывной следящей системы 1-го порядка соответствует передаточной функции апериодического звена:
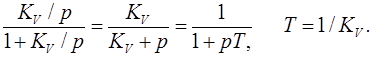
Дифференциальное уравнение непрерывной системы следует из ее структурной схемы (рис. 3):
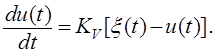
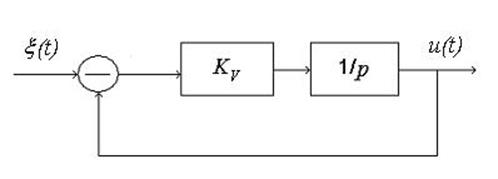
Рис.3
При этом алгоритм работы эквивалентной дискретной следящей системы
также может использоваться для моделирования экспоненциально-коррелированного процесса.
В
отличие от модели (3) здесь воздействие 
не зависит
от постоянной времени 
и для изменения достаточно
установить параметр модели 
(в отличие от 
, процесс является
аппроксимацией непрерывного процесса в виде кусочно-постоянной функции на
интервале временной дискретизации и, поэтому, справедливо соотношение: 
).
2.2. Описание метода моделирования
Моделирование алгоритма выполняется с помощью пакета «Simulink». Схема моделирования показана на рис. 4 (файл для моделирования: «Lab_2_Pr.mdl»). Используются 2 модели: в 1-й модели применяется дискретная следящая система, а во 2-й – модель (3). Оба сформированных процесса поступают в осциллограф «Scope» (для визуального разделения процессов к 2-му процессу добавляется постоянная составляющая с выхода блока «Constant»; величину этой составляющей следует выбрать, исходя из удобства наблюдения 2-х случайных процессов). 1-й процесс также поступает на запись в файл (элемент «To File»). Для того, чтобы получить одинаковые процессы, используются 2 блока «Random Number» (дисперсия, устанавливаемая во 2-м блоке зависит от выбранной постоянной времени).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
