татами
расчета по п.1 (при задании
дисперсии шума в элементе «Random Number» учесть соотношение ![]() Выполнить
моделирование и записать параметры измерителя, а также полученное при
моделирование значение среднего квадрата ошибки.
Выполнить
моделирование и записать параметры измерителя, а также полученное при
моделирование значение среднего квадрата ошибки.
3.
Варьируя параметр ![]() , добиться минимума среднего квадрата ошибки
, добиться минимума среднего квадрата ошибки
измерителя.
Записать значения среднего квадрата ошибки измерителя и параметров ![]() ,
полученные в процессе оптимизации в таблицу (для построения графика).
,
полученные в процессе оптимизации в таблицу (для построения графика).
4.
Повторить выполнение п.3 для параметра ![]() .
.
5. Сопоставить полученные оптимальные параметры с начальными зна-
чениями и, в случае их большого расхождения, выполнить еще одну итерацию оптимизации параметров (повторить пп.3-4 с новыми начальными значениями).
6.
В среде MatLab построить
зависимость ![]() от
от ![]() и
и ![]() дискретной
системы (вариант программы приведен ниже) и найти ее минимум.
дискретной
системы (вариант программы приведен ниже) и найти ее минимум.
%Оптимизация параметров системы с 2 интегратором
clear;
Disp=1000;
A=0.1;
Na=A*A/Disp;
K2=0.0161;
for i=1:1000;
K1=i/1000;
p=Disp*(2*K1*K1+K1*K2+2*K2)/K1/(4-2*K1-K2)+A*A/K2/K2; % Выражение (10)
x(i)=K1;
p11(i)=p;
end;
M=min(p11)
%plot(x,p11)
С
этой целью задать значение ![]() и,
регистрируя минимальное значение
и,
регистрируя минимальное значение ![]() , подобрать
, подобрать ![]() с
точностью до 3-х значащих цифр. Вывести весь массив
с
точностью до 3-х значащих цифр. Вывести весь массив ![]() и по
минимальному значению определить
и по
минимальному значению определить ![]() .
Сопоставить результаты вычислений с помощью программы и результаты
эксперимента.
.
Сопоставить результаты вычислений с помощью программы и результаты
эксперимента.
7.
Повторить пп.1-6 для второго значения ![]() .Учесть
большое значение
.Учесть
большое значение ![]() , требующее выполнения итеративной процедуры оптимизации.
, требующее выполнения итеративной процедуры оптимизации.
Табл.3. Варианты заданий
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1000 |
4000 |
9000 |
16000 |
25000 |
36000 |
4.4. Содержание отчета
1. Схема моделирования.
2.
Результаты расчета для ![]() ,
, ![]() ,
,![]() ,
, ![]() непрерывной
системы и ее дискретного эквивалента
непрерывной
системы и ее дискретного эквивалента
3. Экспериментальные зависимости среднего квадрата ошибки измерите-
ля
от параметров ![]() и значения найденных экспериментально оптимальных
параметров дискретного измерителя (пп.2-5 Задания).
и значения найденных экспериментально оптимальных
параметров дискретного измерителя (пп.2-5 Задания).
4. Результаты вычислений для уточненных значений ![]() дискретной
системы (п.6 Задания).
дискретной
системы (п.6 Задания).
5. Параметры сглаживания.
6. Формулировка задач проведенного исследования и выводы по полу-
ченным результатам.
4.5. Контрольные вопросы
1. Используя
логарифмические характеристики, объяснить влияние параметров ![]() и
и ![]() на суммарную
ошибку измерителя.
на суммарную
ошибку измерителя.
2. Указать ограничения, при которых возможно использование оптимальных параметров, вычисленных для непрерывного аналога.
3. Как влияют параметры моделирования на точность эксперимента?
4. Как влияют параметры измерителя на точность эксперимента?
5.
Объяснить поведение оценки дальности ![]() при пропадании радиосигнала (выход вычитающего
элемента измерителя равен нулю).
при пропадании радиосигнала (выход вычитающего
элемента измерителя равен нулю).
6.
Как выбрать значения параметров ![]() и
и ![]() при
при ![]() ?
?
Практическое занятие №5
Исследование алгоритма комплексирования датчиков высоты
в схеме компенсации
Цель работы – исследование ошибок комплексного алгоритма, содержащего однородные датчики (радиовысотомер и баровысотомер).
5.1. Основные теоретические сведения
Измерители высоты и скорости полета относятся к важнейшим навигационным датчикам на борту летательных аппаратов (ЛА). Баровысотомер измеряет атмосферное давление, зависящее от высоты полета ЛА. Этот датчик устанавливается на всех типах ЛА и движение ЛА в квазигоризонтальном полете обычно выполняется по изобаре, соответствующей постоянному атмосферному давлению. При этом основной считается синоптическая погрешность измерения высоты, обусловленная изменениями метеоусловий. Автокорреляционная функция этой погрешности в случае квазигоризонтального полета описывается косинусоидой, промодулированной экспонентой:
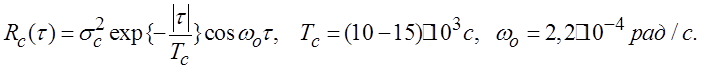
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.