Интегрированные радионавигационные системы: Методические указания к практическим занятиям, страница 14

от дисперсии датчика случайных чисел.

          4. Экспериментальная зависимость дисперсии ошибки  измерителя от интервала корреляции ошибки автономного датчика.

          5. Пояснения к п.6.

          6. Формулировка задач проведенного исследования и выводы по полу-

ченным результатам.

6.5. Контрольные вопросы

1. Сущность принципа инвариантности и основные схемы комплексиро-

вания, реализующие этот принцип?

2. Назначение автономных датчиков воздушной скорости и угла курса?

3. Какими преимуществами обладает комплексный дальномер?

4. Оценку какой величины строит первый интегратор следящей системы

при комплексировании и без него?

5. Почему дисперсия ошибки дальномера без комплексирования оказыва-

ется больше дисперсии ошибки дальномера с комплексированием при идеальном автономном датчике?

Практическое занятие  №7

Моделирование движения объекта на плоскости

Цель работы – исследование метода моделирования движения объекта на плоскости в непрерывном и дискретном времени. Подобное моделирование широко используется при оценке точностных характеристик радиолокационных и радионавигационных систем радиоуправления.

7.1.Описание метода моделирования

При использовании непрерывного времени изменение положения объекта на плоскости (рис.12) можно описать с помощью системы дифференциальных уравнений. Используется модель, в которой координаты объекта  и  изменяются во времени с заданными скоростями и случайными ускорениями.

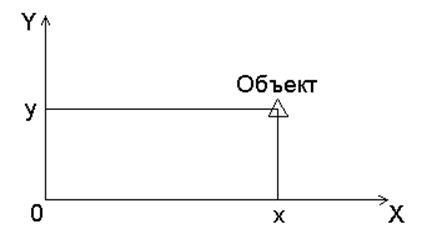
Рис.12

Если проекции ускорения объекта на оси  и  являются независимыми случайными процессами типа «белый» шум, получим систему уравнений

,

,

где  и – проекции вектора скорости объекта на оси  и ;  и  – «белые» шумы со спектральной плотностью .

Система дифференциальных уравнений дополняется начальными условиями при : , ,  и . Значения  и  определяют начальное положение, а  и  – направление и величину вектора скорости объекта.

Моделирование систем радиоуправления и, соответственно, траекторий движения объектов обычно выполняется на цифровых ЭВМ. Для этого задача моделирования должна быть описана в дискретном времени. Система дифференциальных уравнений, с учетом того, что шумы  и  записываются в виде вектора , а наблюдаемыми являются процессы  и , может быть представлена в пространстве состояний уравнениями:

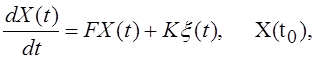
Далее находится решение векторного дифференциального уравнения в виде:

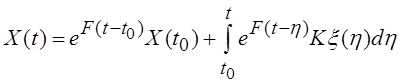
и это решение рассматривается на интервале временной дискретизации  В результате получаем векторное разностное уравнение состояния эквивалентной дискретной модели формирующего фильтра                                                                   

Переходная матрица  вычисляется точным:  или приближенным:   способом. 

Дискретный шум объекта  полагается белым, имеет нулевое среднее и корреляционную матрицу ( - диагональная матрица спектральных плотностей мощности шумов  и  ):                                                                   

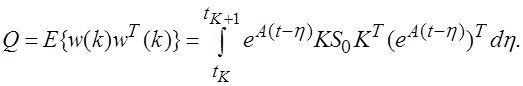
Уравнение измерений в дискретном времени  сохраняет свою форму:

,

причем дискретный шум измерений  также полагается белым, имеет нулевое среднее и корреляционную матрицу                                                                            

Моделирование движения объекта выполняется с помощью пакета Simulink. Схема моделирования в непрерывном времени показана на рис.13 (файл для моделирования: «Lab_5_Tr_Cont.mdl»). Начальные значения проекций вектора скорости  и  устанавливаются с помощью элементов «ConstantX» и «ConstantY», соответственно. Шумы  и  формируются элементами «Band-Limited White Noise» и «Band-Limited White Noise 1». Координаты объекта формируются элементами «IntegratorX»и «IntegratorY» . Для получения траектории движения объекта на плоскости XOY используется индикатор «XYGraph», графики изменения координат xиyможно наблюдать на осциллографе «ScopeX,Y». Для определения дальности  объекта относительно начала координат пара величин х и у преобразуется в комплексное число с помощью элемента «Real-ImagtoComplex» и затем выполняется вычисление модуля с помощью элемента «ComplextoMagnitude-Angle». Для определения угловой координаты  объекта используются элементы «Trigonometric Function» (функция Atan2) и «Fcn» (пересчет угловой координаты из радиан в градусы). Полярные координаты объекта можно наблюдать на осциллографах «ScopeD» и «ScopeA».