Интегрированные радионавигационные системы: Методические указания к практическим занятиям, страница 8

Для входного воздействия в виде аддитивной смеси параболы (с ускорением ) и шума (с эквивалентной спектральной плотностью мощности   ) средний квадрат ошибки системы, включающий в себя квадрат динамической составляющей ошибки   и дисперсию флюктуационной составляющей ошибки ,  определяется выражением:

.

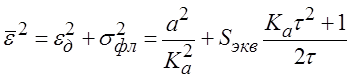Минимизация среднего квадрата ошибки относительно параметров системы приводит к результату:

,

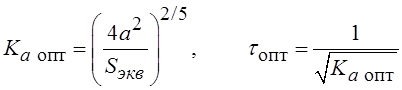где  и  - оптимальные параметры непрерывного измерителя, обеспечивающие минимум среднего квадрата ошибки оценивания координат.

Простейший дискретный эквивалент (с формированием сигнала ошибки с помощью оценки экстраполяции) описывается  в пространстве состояний уравнением:

,

где - вектор оценок координаты и скорости ее изменения;

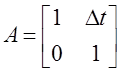;  ;   - вектор параметров, причем .

          Точностные характеристики дискретной системы можно найти, используя как частотную, так и временную область анализа. В частотной области применяется метод z-преобразования. Для системы с 2-мя интеграторами при воздействии с постоянным ускорением дисперсия ошибки в режиме экстраполяции равна:

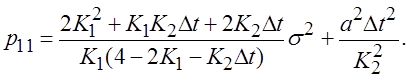                              (10)

Точностные характеристики дискретной и непрерывной систем практически одинаковы, если выполняется условие

,

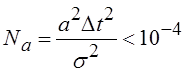где - дисперсия шума в канале измерения.

Сглаживающие свойства следящего измерителя характеризуются параметром:

.

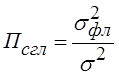Если указанное условие не выполняется, то расчет оптимальных параметров дискретной системы следует уточнить. Такая задача и решается в рамках данной лабораторной работы.

4.2. Описание метода моделирования

          Моделирование схемы следящего измерителя выполняется с помощью пакета «Simulink». Схема моделирования показана на рис.7 (файл для моделирования: «Lab_4_Sl2.mdl»). Динамика изменения координаты моделируется с помощью элемента «Constant», задающего ускорение, и двух интеграторов. К значению координаты добавляется случайная погрешность измерений (элемент «Random Number»). Модель следящего измерителя соответствует приведенному ранее векторному разностному уравнению.

          Ошибка экстраполяции следящего измерителя отображается на экране осциллографа «Scope 1» и отправляется в файл (элемент «To File») для последующей обработки в среде «MatLab».

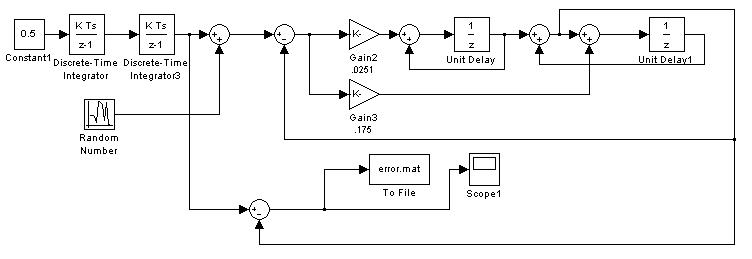
Рис.7

          Параметры моделирования, как и ранее, устанавливаются в разделе меню «Simulation/Configuration parameters» (Type: «Fixed step», Solver: «discrete», время моделирования желательно выбрать большим для получения достоверных статистических результатов моделирования: параметр «Simulation time/Stop time» задается равным 100000). Для начала моделирования дается команда «Simulation/Start». Результаты моделирования наблюдаются в виде осциллограммы, а также передаются в среду «MatLab» для последующей обработки. С этой целью формируется файл с ошибками фильтра err_C. Файл содержит матрицу, состоящую из отсчетов времени t и значений ошибки er. Для выделения строки ошибок er и определения среднего квадрата ошибки используются операторы: er=[0 1]*err_C; mean(er)*mean(er)+var(er). Дисперсия флюктуационной составляющей ошибки определяется оператором var(er). Следует заметить, что статистическая обработка результатов эксперимента также возможна непосредственно при моделировании. Для этой цели подходят элементы: «Math Function» - операция возведения ошибки фильтра в квадрат, «Discrete-Time Integrator» - суммирование квадратов ошибки, «Gain» - деление  на число шагов эксперимента, «Display» - регистрация результата. Однако такой способ обработки результатов эксперимента существенно увеличивает время моделирования и, по этой причине, не рекомендуется его использовать в случае ограниченных временных ресурсов.

4.3. Задание по работе

          1. В среде «MatLab» выполнить расчет оптимальных параметров

 непрерывной системы и, соответствующих им, параметров дискретного эквивалента. Определить значение . Исходные данные  выбрать в соответствии с Табл.3 (, первое значение ).

          2. Установить параметры схемы моделирования в соответствии с резуль-