Исследование аналого-цифрового преобразователя как элемента цифровых автоматических систем: Методические указания к выполнению лабораторной работы № 27

Лабораторная работа № 27

Цель работы: исследование аналого-цифрового преобразователя (АЦП) как элемента цифровых автоматических систем (ЦАС).

1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Возрастание требований к качеству работы систем автоматического управления, увеличение объема перерабатываемой информации, усложнение объектов управления привело к тому, что средствами аналоговой техники и непрерывной автоматики нельзя решить многие практические задачи. В результате в современных системах различного назначения стали широко применяться ЦВМ или специализированные цифровые устройства, позволяющие при небольших массах и габаритах использовать значительно более сложные и эффективные алгоритмы работы.

В системах управления наиболее распространенными входными величинами являются постоянные напряжение и ток, фаза, частота и амплитуда переменных напряжения и тока, линейное и угловое перемещения, временной интервал. Использование микропроцессорных вычислителей и контроллеров, естественно, влечет за собой необходимость преобразовать значения этих величин в цифровые коды, главными особенностями которых являются дискретность во времени и конечное число возможных значений по амплитуде.

На рис.1 приведена типовая структурная схема ЦАС. Входное g(t) и управляемое y(t) воздействия, являющиеся непрерывными величинами, преобразуются к цифровому виду с помощью преобразователей «непрерывная величина – код» (И-К). Дискретность ввода значений в ЦВМ иллюстрируют входные импульсные элементы (ИЭ). Выходная величина ЦВМ также дискретна во времени, что иллюстрирует соответствующий ИЭ. Поскольку объект управления, входящий в непрерывную часть системы, как правило является непрерывным, выходной сигнал ЦВМ подвергается преобразованию «код – непрерывная величина» (К-Н).

Преобразователь «непрерывная величина – код», обычно называемый аналого-цифровым, является одним из наиболее ответственных блоков ЦАС. Основной характеристикой таких преобразователей является характеристика квантования (рис.2). Величину ступеньки называют квантом по амплитуде, и этот квант соответствует цене единицы младшего разряда преобразования. По осям такой характеристики могут быть отложены разные физические величины, но чаще всего – напряжение U и код n (в этом случае говорят о преобразователе напряжения в код).

Число ступенек на характеристике квантования определяется диапазоном изменения входной величины  и значением кванта . Их отношение дает число ступенек характеристики. Это число в аналого-цифровых преобразователях представляется обычно позиционным двоичным или рефлексными кодами. Количество разрядов двоичного кода N, найденное по формуле

                        (1)

где N – ближайшее большее целое – называют разрядностью преобразователя, а  - разрешающей способностью преобразователя или ценой единицы младшего разряда.

            Квантование по амплитуде производится сравнением преобразуемого напряжения с одним или несколькими эталонными. При этом значению преобразуемого сигнала g может быть поставлено в соответствие n квантов, т.е. ближайшее меньшее (такое преобразование называется усечением) или просто ближайшее (так называемое округление).

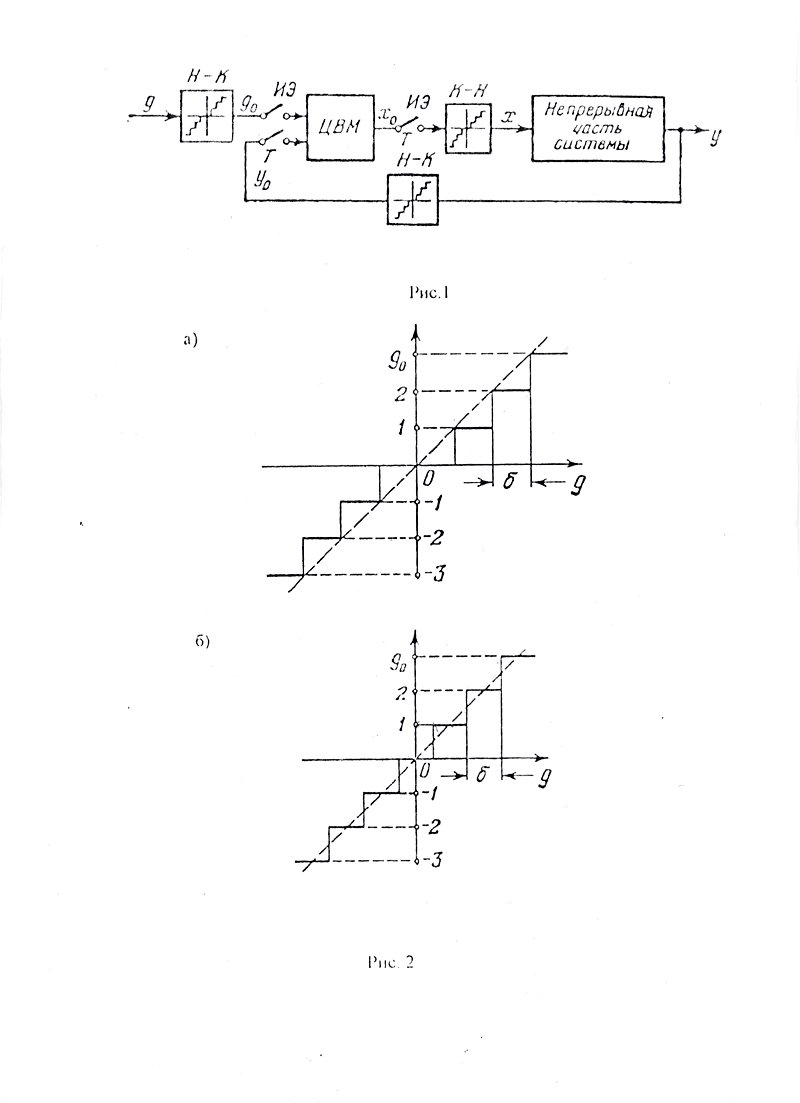
Характеристики квантования для усечения и округления представлены соответственно на рис.2, а и рис.2,б.

            Разница между преобразуемым значением и принятым числом квантов называется ошибкой квантования. Ошибки различны по величине и знаку. В первом случае ошибка положительна и её максимальное значение близко к , во втором – знакопеременна, но не превышает .

            Очевидно, что ЦАС является нелинейной системой уже за счет входных преобразователей. Для её исследования необходимо провести линеаризацию прежде всего указанных преобразователей. Однако обычный для непрерывных САУ метод линеаризации разложением в ряд Тейлора с удержанием только линейного члена оказывается при этом непригодным, поскольку статические характеристики, представленные на рис.2, имеют тангенс угла наклона либо равный нулю, либо стремящийся к бесконечности.

            В то же время, если АЦП входит в контур замкнутой ЦАС, то высокое качество её работы может быть достигнуто только при достаточно малой величине . В этом случае статическую характеристику АЦП можно линеаризовать, проведя некоторую среднюю прямую с крутизной  (пунктир на рис.2), а погрешность от квантования по уровню учесть добавлением во входной сигнал шума квантования, не коррелированного с сигналом. Соответствующая эквивалентная схема представлена на рис.3.