Анализ нелинейных систем. Метод гармонической линеаризации. Применение теории марковских процессов для анализа нелинейных систем

Анализ нелинейных систем

          СУ состоит из отдельных функциональных элементов, для математического описания которых используются типовые элементарные звенья (см. разд. 1.4). Среди типовых элементарных звеньев имеется одно безынерционное (усилительное) звено. Статическая характеристика такого звена, связывающая входную x и выходную y величины, линейна: y=Kx. Реальные функциональные элементы СУ имеют нелинейную статическую характеристику y=f(x). Вид нелинейной зависимости f(∙) может быть разнообразным:

- функции с переменной крутизной (функции с эффектом «насыщения», тригонометрические функции и др.);

- кусочно-линейные функции;

- релейные функции.

          Чаще всего приходиться учитывать нелинейность статической характеристики чувствительного элемента СУ, т.е. нелинейность дискриминационной характеристики. Обычно стремятся обеспечить работу СУ на линейном участке дискриминационной характеристики (если это позволяет вид функции f(∙)) и используют линейную модель y=Kx. Иногда это не удается обеспечить из-за больших значений динамической и флюктуационной составляющих ошибки СУ, либо из-за, так называемой, существенной нелинейности функции f(∙), присущей, например, релейным функциям. Тогда приходится выполнять анализ СУ с учетом звеньев, имеющих нелинейную статическую характеристику, т.е. проводить анализ нелинейной системы.

          Будем считать СУ нелинейной, если она содержит, хотя бы одно звено с нелинейной статической характеристикой.

7.1. Особенности нелинейных систем

          Процессы в нелинейных системах значительно разнообразнее процессов в линейных системах. Отметим некоторые особенности нелинейных систем и процессов в них.

1. Не выполняется принцип суперпозиции: реакция нелинейной системы не равна сумме реакций на отдельные воздействия. Например, независимый расчет динамической и флюктуационной составляющих ошибки слежения, выполненный для линейных систем (см. разд. 3), для нелинейных систем невозможен.

2. К структурной схеме нелинейной системы неприменимо свойство коммутативности (нельзя переставлять местами линейные и нелинейные звенья).

3. В нелинейных системах изменяются условия устойчивости и само понятие устойчивости. Поведение нелинейных систем, с точки зрения их устойчивости, зависит от воздействия и начальных условий. Кроме того, в нелинейной системе возможен новый вид установившегося процесса – автоколебания с постоянными амплитудой и частотой. Такие автоколебания, в зависимости от их амплитуды и частоты, могут и не нарушать работоспособность нелинейной СУ. Поэтому нелинейные системы уже не делятся на два класса (устойчивые и неустойчивые), как линейные системы, а разбиваются на большее количество классов.

          Для нелинейных систем русский математик А.М. Ляпунов в 1892 г. ввел понятия устойчивости «в малом» и «в большом»: система устойчива «в малом», если при некотором (достаточно малом) отклонении от точки устойчивого равновесия она остается в заданной (ограниченной) области ε, и система устойчива «в большом», если она остается в области ε при любом отклонении от точки устойчивого равновесия. Заметим, что область ε можно задать сколь угодно малой вблизи точки устойчивого равновесия, поэтому данное в разд. 2 определение устойчивости линейных систем остается в силе и равноценно определению асимптотической устойчивости по Ляпунову. При этом рассмотренные ранее критерии устойчивости линейных систем для реальных нелинейных систем следует воспринимать как критерии устойчивости «в малом».

4. В нелинейных системах качественно меняются переходные процессы. Например, в случае функции f(∙) с переменной крутизной в нелинейной системе 1-го порядка переходный процесс описывается экспонентой 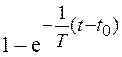 с изменяющимся параметром T.

5. Ограниченная апертура дискриминационной характеристики нелинейной системы является причиной возникновения срыва слежения (система устойчива «в малом»). При этом необходим поиск сигнала и ввод системы в режим слежения (понятие поисково-следящего измерителя дано в разд. 1.1). В системах синхронизации с периодической дискриминационной характеристикой возможны скачки выходной величины.

          Наличие рассмотренных особенностей нелинейных систем приводит к необходимости использования специальных методов для анализа таких систем. Далее рассматриваются:

- метод, основанный на решении нелинейного дифференциального уравнения и позволяющий, в частности, определить ошибку в установившемся режиме, а также полосы захвата и удержания нелинейной системы ФАПЧ;

- методы гармонической и статистической линеаризации, удобные при анализе систем с существенно нелинейным элементом;

- методы анализа и оптимизации нелинейных систем, основанные на результатах теории марковских процессов.

7.2. Анализ регулярных процессов в нелинейной системе ФАПЧ