Анализ нелинейных систем. Метод гармонической линеаризации. Применение теории марковских процессов для анализа нелинейных систем, страница 10

          Флюктуационное возмущение моделируется, в соответствии с (5.25), аддитивным шумом v(t) на выходе дискриминатора. Система  1-го порядка астатизма имеет динамическую ошибку при линейно изменяющемся полезном воздействии. Чтобы учесть эту ошибку, на вход интегратора подается постоянная величина V, соответствующая скорости изменения полезного воздействия (при этом g(t)=0). Особенностью уравнения (7.28) является выбор переменной x(t) таким образом, чтобы она отражала, с точностью до знака, поведение сигнала рассогласования на входе дискриминатора (такой же прием был использован в разд. 7.2). 

          Уравнение Фоккера-Планка-Колмогорова, в соответствии с (7.26), имеет вид:

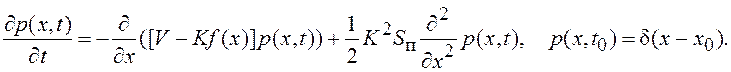(7.29)

          Сначала найдем стационарное распределение  С этой целью интегрируем (7.29) при условии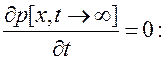

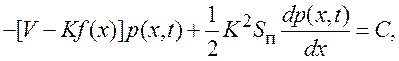                        (7.30)

где постоянная величина С имеет смысл потока плотности вероятности вдоль оси x. Из условия нормировки стационарного распределения 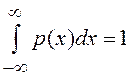 следует:  и 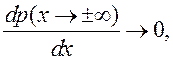 поэтому С=0 (срыв слежения отсутствует). Решение дифференциального уравнения (7.30) имеет вид:

                        (7.31)

причем постоянный коэффициент С₁ определяется из условия нормировки p(x).

          Конкретизируем вид функции f(x). В случае линейной дискриминационной характеристики f(x)=x и V=0 получаем гауссовское распределение:

В случае релейной дискриминационной характеристики f(x)=sign(x) и V=0 распределение отличается от гауссовского:

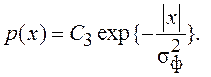
          Теперь, с целью оценки вероятности срыва слежения в нелинейной системе (7.28), займемся решением краевой задачи. Для заданной апертуры дискриминационной характеристики [γ₁, γ₂] запишем граничные условия в виде:

                                   (7.32)

полагая, что границы γ₁ и γ₂ – поглощающие и реализации x(t), достигшие этих границ, выбывают из рассмотрения (происходит срыв слежения). При этом ПВ p(x,t), удовлетворяющая уравнению (7.29) и граничным условиям (7.32), является условной ПВ реализаций x(t), ни разу не достигших границ γ₁ и γ₂.

          Уравнение в частных производных (7.29) содержит две переменные (t и x) и для их разделения используется следующий прием. Представим p(x,t) в виде:

                                            (7.33)

где функция  есть вероятность отсутствия срыва слежения (при  имеем стационарный режим работы системы без срывов).

          Величина Λ в (7.33) характеризует скорость экспоненциального убывания стационарного распределения p(x), причиной которого является отличный от нуля поток плотности вероятности вдоль оси x (через поглощающие границы γ₁ и γ₂).

          Подстановка (7.33) в (7.29) приводит к уравнению:

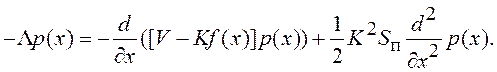           (7.34)

После интегрирования (7.34) по переменной x получаем

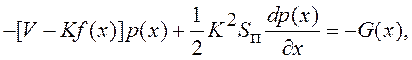                          (7.35)

где G(x) – поток ПВ вдоль оси x (в стационарном режиме без срывов этот поток равен нулю).

          Допустим, что источник изображающих точек (аналоги броуновских частиц), обуславливающих существование потока G(x), расположен вблизи точки x=m_x (значение m_x равно динамической ошибке системы). Тогда слева и справа от этой точки поток G(x) постоянен и равен соответствующим потокам через границы γ₁ и γ₂. При этом вместо уравнения (7.35) можно записать 2 уравнения:

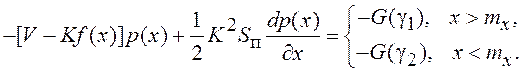           (7.36)

          Величина Λ в (7.33) определяется суммой абсолютных величин потоков через границы γ₁ и γ₂:

          Если динамическая ошибка системы m_x существенно отлична от нуля, то потоком через одну из границ (например, G(γ₂)) можно пренебречь. Поток G(γ₁) определяется в результате решения уравнения (7.36):

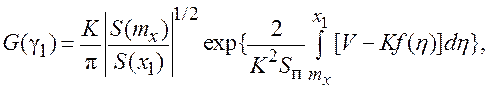           (5.37)

где S(m_x) и S(x₁) – крутизна дискриминационной характеристики в точках устойчивого m_x и, соответственно, неустойчивого x₁ равновесия (рис. 7.16).

          Как следует из выражения (7.37), поток через границу γ₁ определяется, в основном, отношением площади под дискриминационной характеристикой в пределах m_x<x<x₁ к интенсивности флюктуаций на выходе системы 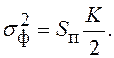    При этом  

          Если динамическая ошибка системы m_x близка к нулю, то потоки через границы γ₁ и γ₂ равны, а Λ определяется из выражения:

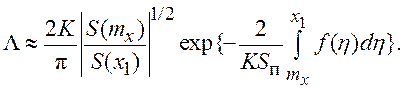
          Вероятность срыва слежения за заданное время t₀ вычисляется по формуле:

                                        (7.38)