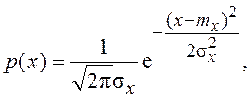Анализ нелинейных систем. Метод гармонической линеаризации. Применение теории марковских процессов для анализа нелинейных систем, страница 6

                                     (7.11)

 где m_x  и   – математическое ожидание и дисперсия случайного процесса x(t).

          Допущение о нормальности случайного процесса x(t) основывается на двух соображениях. Во-первых, случайный процесс x(t) на входе НЭ (т.е. на входе дискриминатора СУ) предварительно прошел через инерционные цепи радиоприемного устройства и, следовательно, подвергся нормализации (следствие центральной предельной теоремы Ляпунова). Во-вторых, результаты статистической линеаризации, как показывают расчеты, характеризуются малой чувствительностью к виду ПВ p(x).

          Сущность метода статистической линеаризации заключается в замене НЭ статистически эквивалентным линейным элементом. Заметим, что такая замена подразумевает аппроксимацию p(y) нормальной ПВ с учетом лишь первых двух вероятностных моментов – математического ожидания m_y и дисперсии  случайного процесса y(t). При этом также предполагается, что случайный процесс y(t) нормализуется, проходя через инерционную линейную часть СУ (инерционность ее должна быть существенно большей, а полоса уже, в сравнении с соответствующими характеристиками цепей радиоприемного устройства).

          Представим входной случайный процесс x(t) в виде суммы математического ожидания m_x и центрированной случайной составляющей x^о(t): x(t)=m_x+x^о(t) и, аналогично, y(t)=m_y+y^о(t). Определим структуру статистически эквивалентного линейного элемента (статистического эквивалента) уравнением, связывающим процесс y₁(t) на его выходе и компоненты входного процесса m_x и x^о(t):

                                                 (7.12)

где K₀ и K₁ – коэффициенты статистической линеаризации для математического ожидания и, соответственно, центрированной случайной составляющей.

          В качестве критерия эквивалентности НЭ и заменяющего его линейного элемента выбирают равенство математических ожиданий и дисперсий:

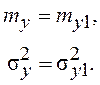                                                      (7.13)

          Коэффициенты статистической линеаризации K₀ и K₁ определяются из (7.12) и (7.13). Математическое ожидание случайного процесса y₁(t) равно m_y1=K₀m_x=m_y, откуда

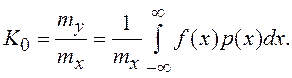                              (7.14)

Дисперсия случайного процесса y₁(t) равна  откуда

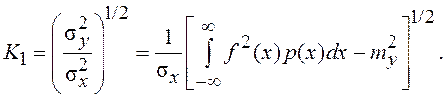          (7.15)

Выражение (7.15) справедливо, если функция y=f(x) возрастает вблизи точки x=m_x, в противном случае следует поменять знак K₁.

          Особенностью метода статистической линеаризации является раздельное прохождение через статистический эквивалент (7.12) математического ожидания m_x и центрированной случайной составляющей x^о(t) с разными коэффициентами усиления K₀ и K₁. Из (7.14) и (7.15) следует, что коэффициенты K₀ и K₁ зависят как от m_x, так и от σ_x: K₀(m_x,σ_x) и K₁(m_x,σ_x) ( в этом проявляется неприменимость к нелинейным системам принципа суперпозиции). Заметим, что из-за зависимости K₀ от m_x статистический эквивалент (7.12) по отношению к математическому ожиданию является нелинейным, а по отношению к центрированной случайной составляющей – линейным.

          В качестве примера рассмотрим задачу определения коэффициентов статистической линеаризации для идеального реле (рис. 7.10).

          Выходной сигнал рассматриваемого НЭ принимает одно из двух значений: c (с вероятностью 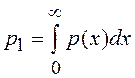) или –c (с вероятностью p₂=1-p₁), поэтому ПВ y(t) представляет собой весовую сумму 2-х δ-функций:

          В соответствии с сущностью метода статистической линеаризации p(y) аппроксимируется нормальной ПВ, характеризуемой значениями m_y и  

          Для определения коэффициента K₀, в соответствии с (7.14), необходимо вычислить

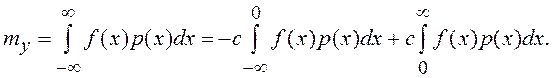
Полагая ПВ p(x) нормальной вида (7.11) и используя замену переменной x:  получаем

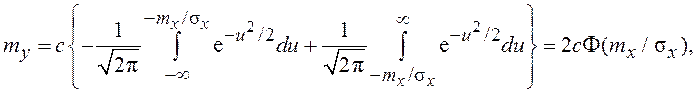
где  – интеграл вероятностей.

          Иногда вместо интеграла вероятностей приходится использовать функцию ошибки 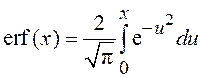 (такая ситуация возникает, например, при расчетах в среде MatLab). Соотношение, связывающее функцию ошибки и интеграл вероятностей: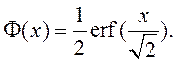

          Таким образом, коэффициент статистической линеаризации для математического ожидания равен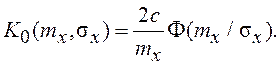  

          На рис. 7.11, а показана зависимость m_y от m_x для нескольких значений σ_x, а на рис. 7.11, б – зависимость K₀(m_x,σ_x) (параметр с=1).