В соответствии с методом статистической линеаризации заменяем НЭ статистическим эквивалентом. Пусть структура статистического эквивалента описывается уравнением (7.12), а критерий эквивалентности определен выражением (7.13). Коэффициенты статистической линеаризации K0(mx,σx) и K1(mx,σx) зависят от вида нелинейности
f(∙), а также от математического ожидания и
среднеквадратического значения случайного процесса x(t) (в
стационарном режиме mx=const и σx=const). Рассматриваем линеаризованную СУ с ПФ в разомкнутом
состоянии 
(для математических ожиданий) и 
(для центрированных случайных составляющих). Далее можно применить
известные методы анализа линейных систем с учетом следующей особенности:
параметры системы зависят от mx и σx, а значения mx и σx зависят от параметров системы. Найти неизвестные
значения mx и σx удобно путем совместного решения уравнений для
динамической составляющей ошибки системы mx и дисперсии случайной составляющей xо(t)
процесса на входе НЭ. Эти уравнения решают методом последовательных приближений
или графическим способом. После нахождения mx и σx нетрудно
вычислить дисперсию флюктуационной составляющей ошибки 
используя известные 
и 
.
В качестве примера рассмотрим задачу анализа
нелинейной системы, содержащей идеальное реле и линейную часть с ПФ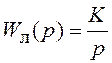 
(заметим, что, в соответствии с результатами разд. 7.3, в
такой системе отсутствуют автоколебания). Пусть шум v(t)
представляет собой экспоненциально-коррелированный процесс со спектральной
плотностью мощности: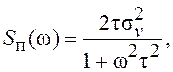 
где 
и 
- дисперсия и интервал корреляции v(t),
зависящие от характеристик радиоприемного тракта.
Линеаризованная система для математических ожиданий описывается
ПФ 
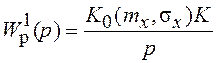и имеет первый порядок астатизма. Следовательно,
при g(t)=const
динамическая составляющая ошибки mx=0. Линеаризованная система для центрированных случайных
составляющих описывается ПФ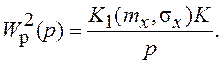 
Дисперсию случайной составляющей xо(t)
процесса на входе НЭ можно найти известным способом (см. разд. 3):
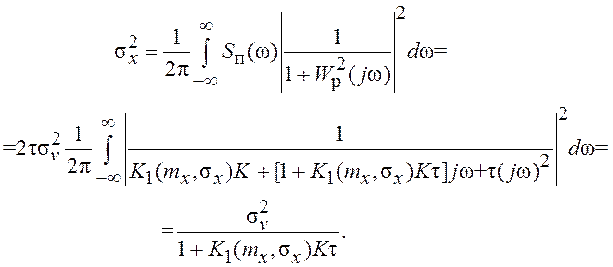(7.23)
При mx=0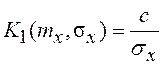 
(см. пример разд. 7.5), поэтому 
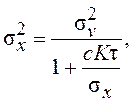откуда 
Заметим, что коэффициент K характеризует
степень инерционности линейной части системы и для нормализации случайного процесса
y(t) требуется выполнение условия Kτ<<1. Поэтому 
(если это не так, метод статистической линеаризации для
анализа системы неприменим).
В случае линейно изменяющегося регулярного воздействия (g(t)=Vt) динамическая составляющая ошибки не равна нулю и определяется с помощью выражения:
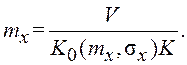(7.24)
Вводим вспомогательную переменную α и представляем выражение (7.24) в виде системы из 2-х уравнений:
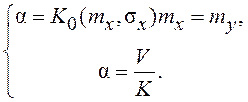
На рис. 7.14, а показано семейство кривых вида 
построенных для десяти значений σx (от σx=0,1
до σx=1,0 с шагом 0,1). Точки пересечения этих кривых и
прямой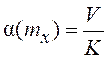 
(V /K=0,2) определяют
зависимость 
(кривая 1 на рис. 7.14, б). Эта
зависимость связывает значения математического ожидания и среднеквадратического
значения случайного процесса x(t) на входе НЭ, удовлетворяющие
уравнению (7.24). Для этих значений определяем коэффициент K1(mx,σx) (по формуле (7.16)
или (7.21)) и, с помощью (7.23), определяем еще одну зависимость (кривая 2 на рис. 7.14, б построена с
использованием формулы (7.16)). Эта зависимость связывает значения
математического ожидания и среднеквадратического значения случайного процесса x(t)
на входе НЭ, удовлетворяющие уравнению (7.23).
Точка пересечения кривых 1 и 2 на рис. 7.14, б
определяет искомые значения 
и 
(
и 
).
Дисперсию флюктуационной составляющей ошибки 
нетрудно найти известным способом (см. разд. 3):
Таким образом, в нашем примере: динамическая составляющая ошибки (при g(t)=Vt, V /K=0,2) равна 0,12, а дисперсия флюктуационной составляющей ошибки (при σv=0,5 и Kτ=0,1) равна 0,044 (размерность соответствует отслеживаемому параметру).
7.7. Применение теории марковских процесссов для анализа нелинейных систем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.