Анализ нелинейных систем. Метод гармонической линеаризации. Применение теории марковских процессов для анализа нелинейных систем, страница 9

          Марковским называется случайный процесс X(t), для которого выполняется следующее условие: если точно известно состояние процесса в момент времени t=t₀, то будущее состояние этого процесса (при t> t₀) не зависит от его прошлого состояния (при t< t₀). Поэтому марковский процесс часто называют «процессом без последействия».

          Случайный процесс, описываемый стохастическим (см. разд. 3) дифференциальным уравнением 1-го порядка является, очевидно, марковским. Случайный процесс, описываемый стохастическим дифференциальным уравнением более высокого порядка, в общем случае, марковским не является. Однако, в большинстве случаев такой процесс можно рассматривать как компоненту векторного случайного процесса, представленного в пространстве состояний. Если случайные воздействия являются белыми шумами, подобный векторный процесс является марковским.

          В случае линейного стохастического векторного дифференциального уравнения случайный процесс является гауссовско-марковским и вероятностные характеристики его определяются вектором математического ожидания и дисперсионной (корреляционной) матрицей. В случае нелинейного стохастического дифференциального уравнения плотность вероятности p[X(t),t] марковского случайного процесса X(t) не является гауссовской.

          Пусть случайный процесс X(t) описывается нелинейным стохастическим дифференциальным уравнением:

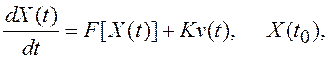                               (7.25)

где F[X(t)] – векторная нелинейная функция компонент X(t); K –некоторый вектор; v(t) – белый шум с известной спектральной плотностью мощности  

          Плотность вероятности p[X(t),t] и динамика ее изменения во времени описывается дифференциальным уравнением в частных производных (уравнением Фоккера-Планка-Колмогорова):

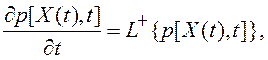                                      (7.26)

где 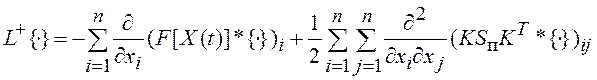  - прямой дифференциальный оператор; x_i, i=1,2,…,n – компоненты вектора X(t); * - оператор умножения; .

          Величина F[X(t)] характеризует скорость изменения математического ожидания процесса X(t) и ее называют коэффициентом сноса; величина  характеризует интенсивность флюктуационных возмущений и ее называют коэффициентом диффузии (такая терминология была предложена при изучении поведения броуновских частиц, распределение координат которых описывается уравнением (7.26); рассматриваемые марковские процессы называют диффузионными). Таким образом, оператор  состоит из 2-х операторов: оператора сдвига (первое слагаемое) и оператора расширения (второе слагаемое) p[X(t),t].

          Уравнение (7.26) дополняется начальным условием

                                                  (7.27)

(если значение  известно точно, то ).

          Решение уравнения (7.26) с начальным условием (7.27) при неограниченной области изменения X(t) называется фундаментальным решением задачи Коши. В частности, можно найти стационарное решение . Уравнение (7.26) полезно также для анализа срыва слежения в нелинейной СУ. Срыв слежения можно рассматривать как выход ошибки слежения за пределы апертуры дискриминационной характеристики [γ₁, γ₂] (если дискриминационная характеристика периодична, как, например, в системе ФАПЧ, выход ошибки слежения за пределы апертуры дискриминационной характеристики приводит к скачку отслеживаемого параметра). При этом вводятся дополнительные ограничения на область изменения X(t) (граничные условия). Решение уравнения (7.26) с начальными и граничными условиями называется решением краевой задачи. Следует отметить, что аналитическое решение указанных задач удается получить только для систем невысокого порядка (). Возможно и численное решение уравнения Фоккера-Планка-Колмогорова с дискретизацией переменной t и квантованием переменной X.

          В качестве примера рассмотрим нелинейную систему, описываемую стохастическим дифференциальным уравнением:

                                 (7.28)

Эта система содержит НЭ (дискриминатор) с характеристикой f(x) и линейную часть с ПФ 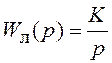 (рис. 7.15); V - скорость изменения полезного воздействия.