Анализ нелинейных систем. Метод гармонической линеаризации. Применение теории марковских процессов для анализа нелинейных систем, страница 3

          Кроме полосы удержания Δf_у, нелинейная система ФАПЧ характеризуется полосой захвата Δf_з  (область начальных расстроек частоты Δω_н, соответствующая переходу системы в режим слежения). В рассматриваемой системе 1-го порядка Δf_з= Δf_у. В случае добавления в структурную схему системы апериодического или пропорционально-интегрирующего звеньев полоса захвата Δf_з  уменьшается: Δf_з≤Δf_у. Для определения Δf_з  следует, в соответствии с рекомендациями разд. 1.9,  описать нелинейную систему в пространстве состояний и найти решение векторного дифференциального уравнения. Задачу удобно решать с помощью численных алгоритмов (например, с помощью алгоритма Рунге-Кутта). Одновременно определяются характеристики переходного процесса. В случае добавления в структурную схему системы идеального интегрирующего звена полоса захвата Δf_з  (и удержания Δf_у) увеличивается до бесконечности. При анализе реальной системы ФАПЧ 2-го порядка астатизма следует учитывать нелинейность интегрирующего звена.

          Заметим, что решение рассмотренных задач можно получить также методом моделирования с использованием средств DesignLab, Simulink и т.п.    

7.3. Метод гармонической линеаризации

Метод гармонической линеаризации, предложенный отечественными учеными Н.М. Крыловым и Н.Н. Боголюбовым (1937 г.) и развитый Л.С. Гольдфарбом (1951 г.), позволяет частотными методами определять условия возникновения автоколебаний в нелинейных системах.

          Рассматривается безынерционное нелинейное звено, которое в дальнейшем будем называть нелинейным элементом (НЭ). На вход НЭ поступает гармонический сигнал x(t)=a sinωt, где a и ω – амплитуда и угловая частота. Выходной сигнал y(t) проходит через узкополосную и, следовательно, инерционную линейную часть системы с ПФ W_л(p) (рис. 7.4), причем выполняется условие:

                           (7.3)

(все гармоники, начиная со второй, хорошо фильтруются линейной частью системы). Полагаем также, что статическая характеристика НЭ f(∙) симметрична, поэтому E{y(t)}=0.

          Сущность метода гармонической линеаризации заключается в замене НЭ эквивалентным линейным элементом. Критерием эквивалентности является равенство амплитуд первой гармоники сигнала на выходе НЭ и сигнала на выходе эквивалентного линейного элемента. При этом влияние высших гармоник, согласно (7.3), не учитывается.

           Гармонический сигнал x(t)=a sinωt, проходя через НЭ, искажается, в зависимости от вида функции y=f(x), и превращается в периодический сигнал y(t)=f(a sinωt). Используем разложение этого сигнала в ряд Фурье:

y(t)=f(a sinωt)=c₀+s₁ sinωt+c₁ cosωt+ s₂ sin2ωt+c₂ cos2ωt+…,

где c₀,c₁,c₂,… и s₁,s₂,… - коэффициенты ряда Фурье.

          Допущение о симметрии функции y=f(x) относительно начала координат позволяет не учитывать постоянную составляющую в выходном сигнале y(t):

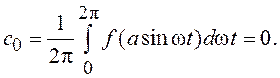
          Гармониками, начиная со второй, пренебрегаем, рассчитывая на фильтрующие свойства линейной части системы. Поэтому

                                    (7.4)

где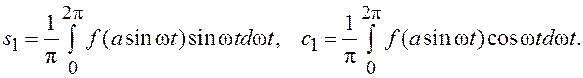

          Выражение  (7.4) позволяет найти приближенную линейную зависимость y от x:

                 (7.5)

где q(a)=s₁/a; q^’(a)=c₁/a.

          Операция замены нелинейной зависимости y=f(x) на приближенную линейную зависимость (7.5) называется гармонической линеаризацией, а q(a) и q^’(a) называются коэффициентами гармонической линеаризации. Применим к (7.5) преобразование Лапласа:

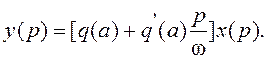
Определим эквивалентную ПФ НЭ:

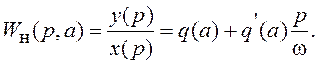
Подстановкой p=jω находим частотную эквивалентную ПФ НЭ:

                                            (7.6)

которая для безынерционного НЭ является функцией только амплитуды. Модуль эквивалентной ПФ НЭ

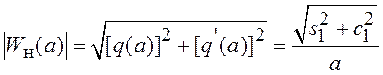
равен отношению амплитуды первой гармоники сигнала на его выходе () к амплитуде входного сигнала a. Аргумент эквивалентной ПФ НЭ 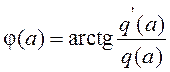 определяет фазовый сдвиг первой гармоники сигнала на выходе НЭ относительно входного сигнала.

          В случае однозначной нелинейной зависимости y=f(x) эквивалентная ПФ НЭ чисто вещественна ( и φ(a)=0).

          Эквивалентная ПФ НЭ W_н(a) может быть изображена графически на комплексной плоскости в виде годографа, который называют эквивалентной АФХ НЭ. В задаче определения условий возникновения автоколебаний в нелинейной системе будет полезна обратная АФХ НЭ (со знаком минус):  (см. разд. 7.4).