Решение уравнения (7.43) оказывается еще более
сложной задачей в сравнении с решением уравнения Фоккера-Планка-Колмогорова.
Поэтому обычно ищут приближенное решение для гауссовской аппроксимации ![]() . При этом дифференциальное уравнение в частных производных (7.43) заменяется эквивалентной
системой дифференциальных уравнений для первых 2-х моментов
. При этом дифференциальное уравнение в частных производных (7.43) заменяется эквивалентной
системой дифференциальных уравнений для первых 2-х моментов ![]() :
:
 (7.44)
(7.44)
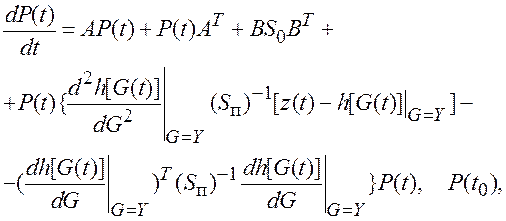 (7.45)
(7.45)
где 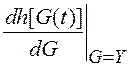 представляет собой строку, а
представляет собой строку, а 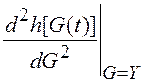 - матрицу.
- матрицу.
Уравнения (7.44) и (7.45)
определяют структуру и параметры системы, оценивающей компоненты G(t)
с минимальной дисперсией ошибки. Приближенное решение уравнения (7.43) тем
точнее, чем больше отношение сигнал/шум, выше инерционность линейной части
системы и ближе априорное распределение ![]() к гауссовскому.
к гауссовскому.
Особенности алгоритма оценивания (7.44) и (7.45):
1) уравнение (7.44), определяющее структуру системы, содержит в правой части нелинейное преобразование (формирование наблюдаемой компоненты Y(t)) и совпадает с соответствующим уравнением расширенного фильтра Калмана (см. разд. 5);
2) в правой части дисперсионного
уравнения (7.45) присутствует наблюдение z(t), поэтому весовой
коэффициент системы 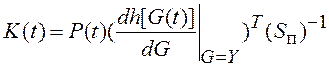 зависит от конкретной реализации z(t);
в случае высокой точности оценивания (при большом отношении сигнал/шум)
слагаемое в правой части (7.45), содержащее z(t), можно исключить
и, тогда, уравнение (7.45) совпадет с соответствующим уравнением расширенного
фильтра Калмана;
зависит от конкретной реализации z(t);
в случае высокой точности оценивания (при большом отношении сигнал/шум)
слагаемое в правой части (7.45), содержащее z(t), можно исключить
и, тогда, уравнение (7.45) совпадет с соответствующим уравнением расширенного
фильтра Калмана;
3) в случае линейного закона
модуляции радиосигнала (![]() ) уравнения (7.44) и (7.45)
соответствуют алгоритму фильтра Калмана;
) уравнения (7.44) и (7.45)
соответствуют алгоритму фильтра Калмана;
4) для вычисления производных 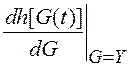 необходимо знать все параметры радиосигнала (информационные и
неинформационные), поэтому в вектор состояния формирующего фильтра G(t)
включают все неизвестные параметры и, соответственно, оценивают их (оценка
неинформационных параметров радиосигнала создает благоприятные условия для
оценивания информационных параметров);
необходимо знать все параметры радиосигнала (информационные и
неинформационные), поэтому в вектор состояния формирующего фильтра G(t)
включают все неизвестные параметры и, соответственно, оценивают их (оценка
неинформационных параметров радиосигнала создает благоприятные условия для
оценивания информационных параметров);
5) если апостериорное распределение ![]() полимодальное, то уравнения (7.44) и (7.45) используют в предположении,
что при поиске сигнала выделен истинный локальный максимум
полимодальное, то уравнения (7.44) и (7.45) используют в предположении,
что при поиске сигнала выделен истинный локальный максимум ![]() .
.
В качестве примера рассмотрим задачу оценивания фазы радиосигнала. Уравнение наблюдения определяется видом принимаемого радиосигнала:
![]()
где a и ω0 – амплитуда и частота радиосигнала (полагаем их известными величинами, иначе они подлежат оцениванию); φ(t) – фаза радиосигнала (информационный параметр); v(t) – ошибка наблюдения, обусловленная шумом входных цепей радиоприемного устройства.
Оцениваем только информационный параметр, поэтому 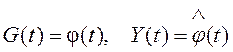 . При этом
. При этом ![]() Необходимо задать динамику изменения оцениваемого
параметра, представив его в виде марковского случайного процесса. Пусть
поведение φ(t) описывается
с помощью экспоненциально-коррелированного случайного процесса, определяемого
уравнением:
Необходимо задать динамику изменения оцениваемого
параметра, представив его в виде марковского случайного процесса. Пусть
поведение φ(t) описывается
с помощью экспоненциально-коррелированного случайного процесса, определяемого
уравнением:
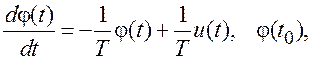
где T – постоянная времени формирующего фильтра,
характеризующая интервал корреляции φ(t); u(t) – белый шум с известной СПМ ![]() , причем дисперсия φ(t)
равна
, причем дисперсия φ(t)
равна 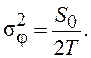
Вычисляем производную нелинейного преобразования h[φ(t)]:

В соответствии с (7.44) записываем алгоритм оценивания фазы радиосигнала:
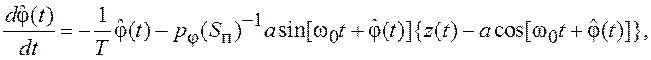 (7.46)
(7.46)
где pφ – дисперсия ошибки оценивания фазы.
Рассмотрим второе слагаемое в правой части (7.46):
![]()
Используя тригонометрическое соотношение
![]() и фильтрующие
свойства линейной части системы (пренебрегаем второй гармоникой), получаем:
и фильтрующие
свойства линейной части системы (пренебрегаем второй гармоникой), получаем:
![]() (7.47)
(7.47)
где ![]() - коэффициент усиления.
- коэффициент усиления.
Из (7.46) и (7.47) следует, что в системе
оценивания фазы наблюдение z(t) умножается на опорный сигнал ![]() и результат с коэффициентом K1(t)
корректирует состояние линейной части системы.
и результат с коэффициентом K1(t)
корректирует состояние линейной части системы.
Вычисляем 2-ю производную нелинейного преобразования h[φ(t)]:
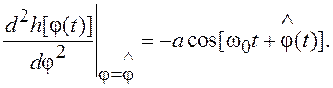
В соответствии с (7.45) записываем дисперсионное уравнение:
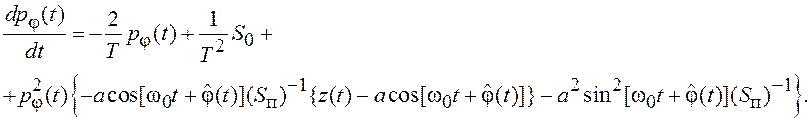
Используя тригонометрическое соотношение
![]() и
фильтрующие свойства линейной части системы, получаем:
и
фильтрующие свойства линейной части системы, получаем:
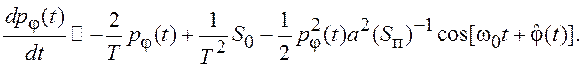 (7.48)
(7.48)
Полагая точность оценивания фазы достаточно высокой
(используется допущение о большом отношении сигнал/шум), найдем дисперсию
ошибки оценивания фазы в стационарном режиме ![]() В этом случае
В этом случае 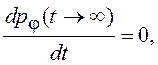 а
а ![]() и необходимо решить алгебраическое
уравнение
и необходимо решить алгебраическое
уравнение 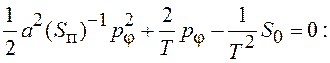
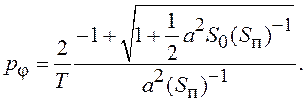
Коэффициент усиления системы с постоянными параметрами, обеспечивающими минимум дисперсии ошибки оценивания в стационарном режиме, равен
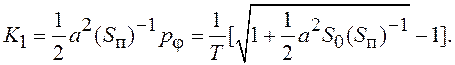
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.